SEGUNDA SESION DE CLASE

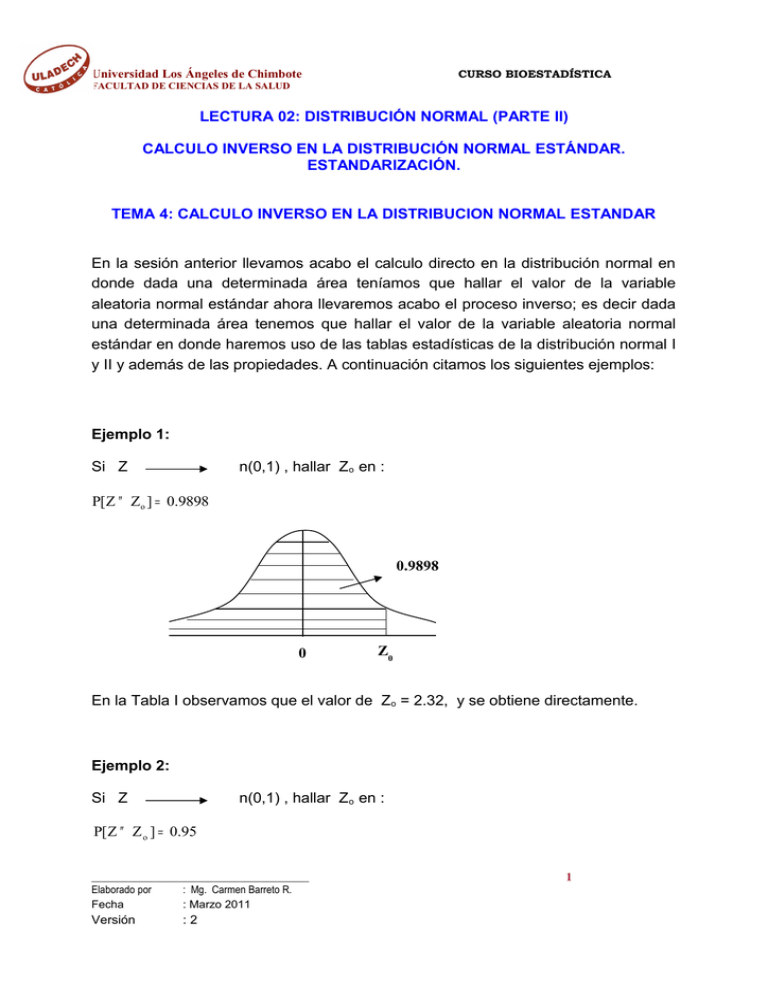
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
LECTURA 02: DISTRIBUCIÓN NORMAL (PARTE II)
CALCULO INVERSO EN LA DISTRIBUCIÓN NORMAL ESTÁNDAR.
ESTANDARIZACIÓN.
TEMA 4: CALCULO INVERSO EN LA DISTRIBUCION NORMAL ESTANDAR
En la sesión anterior llevamos acabo el calculo directo en la distribución normal en
donde dada una determinada área teníamos que hallar el valor de la variable
aleatoria normal estándar ahora llevaremos acabo el proceso inverso; es decir dada
una determinada área tenemos que hallar el valor de la variable aleatoria normal
estándar en donde haremos uso de las tablas estadísticas de la distribución normal I
y II y además de las propiedades. A continuación citamos los siguientes ejemplos:
Ejemplo 1:
Si Z
n(0,1) , hallar Zo en :
P[Z ≤ Zo ] = 0.9898
0.9898
0
Z0
En la Tabla I observamos que el valor de Zo = 2.32, y se obtiene directamente.
Ejemplo 2:
Si Z
n(0,1) , hallar Zo en :
P[ Z ≤ Z o ] = 0.95
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
1
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
0.95
0
Z0
En la Tabla I observamos que el valor Z o se encuentra entre 1.64 y 1.65 y llevamos
acabo el proceso de interpolación:
Z
1.64
Zo
1.65
Area
0.9495
0.95
0.9505
0.9505 − 0.9495
1.65 − 1.64
=
0.95
− 0.9495
Z0 − 1.64
0.001
0.01
=
0.0005 Z0 − 1.64
Aplicando la regla de tres simples obtenemos :
Z0 = 1.645
Ejemplo 3:
Si Z
n(0,1) , hallar el valor – Z o en:
P[ Z ≤ Z o ] = 0.01
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
2
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
0.01
-Zo
0
En la Tabla I observamos que el valor Z o se encuentra entre -2.33 y -2.32 y llevamos
acabo el proceso de interpolación:
Z
-2.33
- Zo
-2.32
Area
0.0099
0.01
0.0102
0.0099 − 0.0102
− 2.33 − ( − 2.32)
=
0.01 − 0.0099
− Z 0 − ( − 2.32)
− 0.0003
0.01
=
0.0001 − Z 0 + 2.32
Aplicando la regla de tres simples obtenenmos :
− Z0 = − 2.3267
Ejemplo 4:
Si Z
n(0,1), hallar el valor de Z o en:
P[ Z ≥ Z o ] = 0.10
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
3
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
0.10
0
Zo
Aplicando propiedad:
P[ Z ≥ Z o ] = 1 − P[ Z < Z o ]
P[ Z < Z o ] = 0.90
En la Tabla I observamos que Zo se encuentra entre 0.8997 y 0.9015 y llevamos
acabo el proceso de interpolación:
Z
1.28
Zo
1.29
Area
0.8997
0.90
0.9015
0.9015 − 0.8997
1.29 − 1.28
=
0.90 − 0.8997
Z0 − 1.28
0.0018
0.01
=
0.0003 Z0 − 1.28
Aplicando la regla de tres simples obtenenmos :
Z0 = 1.282
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
4
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
Ejemplo 5:
Si Z
n(0,1), hallar el valor de -Z 0 y Z0 simétricos en:
P[− Z o ≤ Z ≤ Z o ] = 0.90
0.90
- Zo
Zo
0
En la Tabla II observamos que Z o se encuentra entre 0.8990 y 0.9011 y llevamos
acabo el proceso de interpolación:
Z
1.64
Zo
1.65
Area
0.8990
0.90
0.9011
0.9011 − 0.8990
1.65 − 1.64
=
0.90
− 0.8990
Z0 − 1.64
0.0021
0.01
=
0.001 Z 0 − 1.64
Aplicando la regla de tres simples obtenenmos :
Z0 = 1.645
y
− Z0 = − 1.645
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
5
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
Ejemplo 6:
Si Z
n(0,1) , hallar los valores -Zo y
Zo simétricos en:
P[− Z o ≤ Z ≤ Z o ] = 0.95
0.95
- Zo
0
Zo
En la Tabla II observamos que se encuentra el área dada, por lo tanto no es
necesario interpolar.
Entonces –Zo=-1.96
y
Zo= 1.96
TEMA 5: ESTANDARIZACION DE UNA VARIABLE ALEATORIA NORMAL
Dada una variable aleatoria normal X, con media μ y desvío σ, si definimos otra
X− µ
variable aleatoria Z =
entonces la variable aleatoria Z tendrá una distribución
σ
normal estándar.
Al usar la fórmula de transformación cualquier variable aleatoria normal X se
convierte en una variable aleatoria normal estandarizada Z. Mientras los datos
originales para la variable aleatoria X tenían una media y una desviación estándar, la
variable aleatoria estandarizada Z siempre tendrá una media μ = 0 y
una
desviación estándar σ = 1.
Veremos algunos ejemplos:
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
6
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
Ejemplo 1:
Si
X → n (100,100) , hallar:
a)
P[X ≤ 120]
120 − 100
]
10
P[X ≤ 120] = P[ Z ≤ 2] = 0.9772
P[X ≤ 120] = P[ Z ≤
D.N.G
0.9772
120
100
D.N.E.
0.9772
0
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
2
7
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
b)
P[X ≥ 130]
130 − 100
]
10
P[X ≥ 130] = 1 − P[ Z < 3]
P[X ≥ 130] = 1 − 0.9987
P[X ≥ 130] = 0.0013
P[X ≥ 130] = 1 − P[ Z <
D.N.G.
0.0013
100
130
D.N.E.
0.0013
0
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
3
8
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
c) P[X < 75]
75 − 100
]
10
P[X < 75] = P[ Z < − 2.5]
P[X < 75] = 0.062
P[X < 75] = P[ Z <
D.N.G.
0.0062
75
100
D.N.E.
0.0062
-2.5
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
0
9
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
d)
P[75 ≤ X ≤ 125]
75 − 100
130 − 100
Z<
]
10
10
P[75 ≤ X ≤ 125] = P[− 2.5 ≤ Z ≤ 2.5]
P[75 ≤ X ≤ 125] = 0.9878
P[75 ≤ X ≤ 125] = P[
NOTA: UTILIZAR LA TABLA II DIRECTAMENTE
D.N.G.
0.9878
75
125
100
D.N.E.
0.9878
- 2.5
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
0
2.5
10
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
e) P[80 ≤ X ≤ 134]
80 − 100
134 − 100
Z<
]
10
10
P[− 2.00 ≤ Z ≤ 3.4]
P[ Z ≤ 3.4] − P[ Z < − 2.00]
0.9997 − 0.0228
0.9767
P[80 ≤ X ≤ 134] = P[
P[75 ≤
P[75 ≤
P[75 ≤
P[75 ≤
X≤
X≤
X≤
X≤
125] =
125] =
125] =
125] =
D.N.G.
0.9767
80
100
134
D.N.E.
0.9767
-2.00
_________________________________________
Elaborado por
: Mg. Carmen Barreto R.
Fecha
: Marzo 2011
Versión
:2
0
3.4
11