SESION DE APRENDIZAJE N° 5

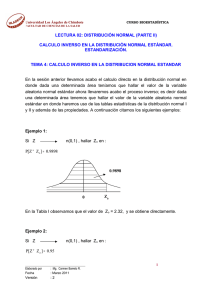
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
LECTURA 03: DISTRIBUCIÓN T STUDENT Y DISTRIBUCIÓN CHICUADRADO
TEMA 6: DISTRIBUCION T STUDENT. MANEJO DE TABLAS ESTADISTICAS.
1.
INTRODUCCION
Se dice que una variable aleatoria T tiene una distribución t de student con υ grados
de libertad, si su función de densidad de probabilidad está dada por:
f (t ) =
 υ + 1
γ 

2 − (υ + 1) / 2
 2   1+ t 


υ 
υ 
υπ γ   
 2
t∈ R
y
υ = 1, 2 ,.....
Se denota como: T 
tv
y se lee la variable T se distribuye como una t de student
con υ grados de libertad.
OBSERVACIONES
La distribución de la variable aleatoria T depende únicamente del parámetro υ .
Entonces, hay una distribución t correspondiente a cada grado de libertad. En la fig.
10 se presenta un bosquejo de la función de densidad de la variable aleatoria T,
para diferentes grados de libertad. En la misma figura se da la gráfica de la normal
estándar. Note, la simetría de la distribución t alrededor de t=0 y varía de menos
infinito a más infinito.
La media y la varianza de la distribución t student con υ grados de libertad están
dados por:
M = E (T ) = 0 , v > 1
σ
2
= V (T ) =
v
v− 2
, v> 2
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
1
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
fig. 7
Como podemos ver la distribución t de student es muy similar a la distribución
normal n(0,1), ya que ambas tiene como dominio todas las reales, son simétricas
con respecto a su media cero. Las dos tienen gráficos de forma de campana, pero la
distribución t de student tiene mayor dispersión que la distribución normal n(0,1). La
distribución t de student se aproxima a la normal n(0,1), cuando el grado de libertad
υ es suficientemente grande. En la práctica, cuando el grado de libertad υ es mayor
o igual que 30 ( υ ≥ 30), la distribución t se trata como distribución normal n(0,1).
2. MANEJO DE TABLAS ESTADISTICAS.
Debido a la importancia de la distribución t en la inferencia estadística y la dificultad
para evaluar la función de distribución de la variable aleatoria T, estas se dan en una
tabla. En las tablas III y IV se presentan áreas de esta distribución para diferentes
grados de libertad. Para el cálculo de áreas de la distribución t de student se utilizan
las mismas propiedades para el calculo de áreas en de la distribución normal n(0,1).
a)
Uso de la Tabla III: Calcula la probabilidad que la variable aleatoria T tome
valores menores o iguales a una constante t 0 = t 1− α . Así:
P [ T ≤ t1− α ] = 1 − α
1-α
0
fig. 8
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
t1- α
α
2
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
Ejemplo 1:
0.975
Si T  t18, hallar:
1-α
a) P[T < 2.101] = 0.975
α
0
2.101
Se desea hallar el área para valores menores que 2.101 (P[T<2.101]) en una
distribución t student con 18 grados de libertad. Para este tipo de área requerida
utilizaremos la Tabla III . En primer lugar debemos ubicar los grados de libertad (18)
en el lado izquierdo de la tabla y luego avanzar hacia la derecha en la misma
dirección y ubicar el valor 2.101 y hallar el área (probabilidad) en la parte superior de
dicho número, tal como se muestra a continuación:
TABLA III
α
1- α
υ
0.10
0.90
0.05
0.95
0.025
0.975
t0.90
t0.95
t0.975
1
2
.
.
.
18
.
.
.
500
...
0.001
0.999
t0.999
2.101
∞
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
3
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
b) P[T > 1.330] = 1 − P[T ≤ 1.330] = 1 − 0.90
P[T > 1.330] = 0.10
0.10
0
1.330
En este ejemplo aplicamos la propiedad respectiva que se usa para el cálculo de
otras áreas de la distribución normal estándar (sesión de aprendizaje 1) y hallamos
el área que corresponde a P[T ≤ 1.330] = 0.90 , tal como se muestra a continuación:
α
1- α
υ
1
2
.
.
.
18
.
.
.
500
0.10
0.90
t0.90
TABLA III
0.05
0.95
t0.95
0.025
0.975
...
0.001
0.999
t0.975
t0.999
1.330
∞
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
4
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
c) P[T ≤ − 1.330] = P[T ≥ 1.330]
P[T ≤ − 1.330] = 1 − P[T < 1.330]
P[T ≤ − 1.330] = 1 − 0.90 = 0.10
0.10
-1.330
0
d) P[T > − 1.330] = P[T < 1.330] = 0.90
0.90
-1.330
b)
0
Uso de la Tabla IV: Calcula la probabilidad que la variable aleatoria T tome
valores entre dos puntos simétricos − t 0 = − t 1− α / 2 y t 0 = t1− α / 2 . Así:
α/2
α/2
1-α
-to
0
to
fig. 9
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
5
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
Ejemplo 2:
Si T  t18, hallar:
a) P[ − 2.101 < T < 2.101] = 0.95
0.95
-2.101
0
2.101
Se desea obtener el área para valores comprendidos entre -2.101 y 2.101 [P [2.101<T<2.101] para una distribución t Student con 18 grados de libertad. Cabe
indicar que los puntos son simétricos y que en este caso debemos utilizar la Tabla
IV. En primer lugar debemos ubicar los grados de libertad (18) en el lado izquierdo
de la tabla y luego avanzar hacia la derecha en la misma dirección y ubicar el valor
2.101 y hallar el área (probabilidad) en la parte superior de dicho número, tal como
se muestra a continuación:
TABLA IV
α
1- α
υ
0.10
0.90
t0.955
1
2
.
.
.
18
.
.
.
500
∞
0.05
0.95
t0.975
0.02
0.98
0.001
0.999
t0.99
t0.995
2.101
____________________________________________
Elaborado por
Fecha
Versión
...
: Mg. Carmen Barreto R.
: Marzo 2011
:2
6
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
b) P[ − 2.878 ≤ T ≤ 2.878] = 0.99
0.99
-2.878
0
2.878
TEMA 7: DISTRIBUCION CHI CUADRADO. MANEJO DE LA TABLAS
ESTADISTICAS.
1. INTRODUCCIÓN
Se dice que la variable aleatoria X tiene una distribución chi cuadrado con υ grados
de libertad, si su función de densidad está dada por:
−v
22
X 2e
 v
ρ 
 2
−v
2
;
si
;
si
x≥ 0
f (x) =
0
x < 0
Notación abreviada:
X  X2υ
Donde υ es un número entero positivo.
2.
MANEJO DE TABLAS ESTADISTICAS.
Debido a que la distribución chi-cuadrado es importante en las aplicaciones,
principalmente en inferencia estadística alguna de las cuales citaremos
posteriormente; la función de distribución F(x) están preparadas en tablas (ver Tabla
V), para valores seleccionados de v y X2. Por lo tanto, se puede encontrar en la
2
tabla, la probabilidad que la variable aleatoria X que tiene una distribución X v
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
7
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
2
2
(1 ≤ v ≤ 30) sea menor o igual a un valor constante X 0 = X1− α representado por:
P[ X < X 12− α , v ] = 1 − α
1-α
α
X12− α ,v
0
fig. 10
Como no existe simetría la Tabla V presenta las probabilidades acumuladas (áreas)
2
desde X 0 = 0 hasta X 02  ∞.
Puesto que existe una distribución chi-cuadrado diferente para cada valor de υ,
resulta impráctico proporcionar tablas de áreas completas. En lugar de esto la Tabla
V presenta un resumen de la información más esencial acerca de la distribución.
Para calcular áreas en la distribución chi cuadrado también se deben usar las
propiedades dadas para el cálculo de áreas en la distribución normal.
Ejemplo 3:
Si X → X 220 , hallar:
a) P[ X ≤ 28.4] = 0.90
0.90
0
28.4
Se desea hallar el área (probabilidad) para valores menores o iguales que 28.4
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
8
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
[P[X < 28.4]] con 20 grados de libertad. Para hallar este tipo de área utilizaremos la
Tabla V. En primer lugar debemos ubicar los grados de libertad (20) en el lado
izquierdo de la tabla y luego avanzar hacia la derecha en la misma dirección y ubicar
el valor 28.4 y hallar el área (probabilidad) en la parte superior, tal como se muestra
a continuación:
TABLA V
υ
X2 0.995
X20.99
1
2
3
.
.
.
20
.
.
.
100
X20.975
X20.95
X20.90
....
28.4
b) P[ X ≥ 12.4] = 1 − P[ X < 12.4]
P[ X ≥ 12.4] = 1 − 0.10
P[ X ≥ 12.4] = 0.90
0.90
0
12.4
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
9
X20.005
Universidad Los Ángeles de Chimbote
CURSO BIOESTADÍSTICA
FACULTAD DE CIENCIAS DE LA SALUD
c) P[12.4 ≤ X ≤ 28.4] = P[ X ≤ 28.4] − P[ X < 12.4]
P[12.4 ≤ X ≤ 28.4] = 0.90 − 0.10
P[12.4 ≤ X ≤ 28.4] = 0.80
0.80
0
12.4
28.4
____________________________________________
Elaborado por
Fecha
Versión
: Mg. Carmen Barreto R.
: Marzo 2011
:2
10