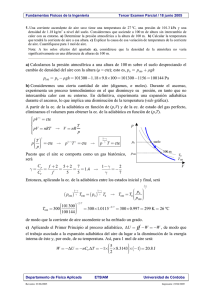
π ε ε πε
Anuncio

DISTRIBUCIÓN ESFÉRICA (Esfera maciza) Una carga Q se encuentra uniformemente distribuida en todo el volumen de una esfera no conductora de radio R . Determinar el campo eléctrico en puntos: 1. fuera de la esfera, r > R 2. dentro de la esfera, r ≤ R Fig. 12 SOLUCIÓN v 1. En la figura 12 se muestran las líneas de campo eléctrico E , suponiendo la esfera cargada positivamente, y se muestran también las superficies gaussianas para r > R y r < R , las cuales consisten de esferas centradas en la esfera cargada. De la ley de Gauss, εo ∫ E ⋅ ds = Q cuando r > R la carga que encierra la superficie gaussiana es exactamente Q . Debido a la simetría esférica, ε o E ∫ ds = Q ε o E (4π r 2 ) = Q Y despejando E tenemos E= Q 4πε 0 r 2 r >R Lo mismo que obtendríamos si la carga Q fuese una carga punto colocada en el centro de la esfera. 2. r < R Para esta situación, la carga Q' encerrada por la superficie gaussiana es menor que Q , y será 4 Q' = ρV ' = ρ ( π r 3 ) 3 Donde ρ es la densidad de carga y V ' es el volumen encerrado por la carga Q' Como c a rga total Q Q = ρ= = V volumen esfera 4 π R3 3 resulta 3Q , y, ρ= 4π R 3 4 Q 4 r3 3 3 Q' = ρ ( π r ) = ( π r )=Q 3 4 3 3 3 R πR 3 De la ley de Gauss ε o ∫ E ⋅ d s = Q' r3 ε o E (4π r ) = Q 3 R Q r E= 4πε o R 3 2 , r<R Observe que el campo es cero para r = 0 , y aumenta linealmente con r hasta r = R , y después decrece inversamente a r 2 , es decir, E= r , E α r , para r < R , 4πε o R 3 E= 1 Q , Eα , para r > R 4πε o r 2 r2 Los campos coinciden en muestran en la figura 13. Q y, 1 r = R y tienen el valor E = 1 Q ; y sus curvas se 4πε o R 2 Fig. 13