ANÁLISIS DE DATOS Pruebas de Hipótesis Consisten en comparar
Anuncio

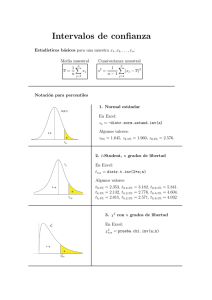
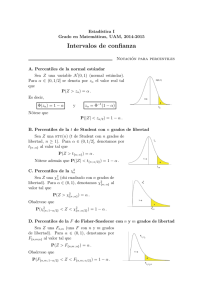
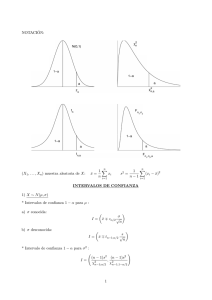
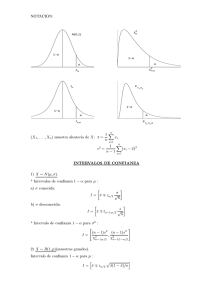
ANÁLISIS DE DATOS Pruebas de Hipótesis Consisten en comparar un parámetro poblacional (propuesto o hipotetizado) con su estimador obtenido a través de una muestra y cuantificar la probabilidad de que esta muestra provenga o no de esa población. De otro modo: Se trata de señalar en términos de probabilidad: qué tan lejos un estimador de un parámetro puede estar desde el parámetro de modo que resulte o no una diferencia estadísticamente significativa. Definición: Valor p = es la probabilidad de obtener un valor tan extremo o más extremo que aquel valor límite que incluye el rango de aceptación de la hipótesis nula y que si es tan pequeño se puede llegar a decir que no hay evidencia para aceptar Ho. De otro modo: Si es la probabilidad de rechazar Ho cuando es verdadera (error tipo I ), la regla de decisión para aceptar o rechazar una hipótesis en función del valor p, es: si p < rechazo Ho si p > acepto Ho Nota: en un test de dos lados (caso bilateral) p = 2 a_dat115/jsc ANÁLISIS DE DATOS Pruebas de Hipótesis Ejemplo (caso bilateral): En un examen aplicado a una gran cantidad de alumnos de diferentes escuelas, la media de las calificaciones fue de 74,5 y la desv.st. = 8. En una escuela de 100 alumnos se ensayó un nuevo procedimiento de enseñanza y se encontró una media muestral de 75,9. Se desea probar que el nuevo procedimiento de enseñanza es diferente al que se está aplicando en todas las escuelas. Considerar un nivel de confianza del 95% Ho : no hay diferencias ==> -1,96 <= Z/2 <= 1,96 H1: hay diferencias ==> Z/2 < -1,96 o Z/2 > 1,96 Z = (75,9 - 74,5) / ( 8 / 1001/2 ) = 1,75 Z se encuentra en la región de aceptación ( -1,96 <= 1,75 <= 1,96 ) con un valor de p = 2x0,04 = 0,08 Luego: se acepta Ho, no hay diferencias significativas entre ambos procedimientos de enseñanza. a_dat116/jsc ANÁLISIS DE DATOS Pruebas de Hipótesis Ejemplo (caso unilateral): En la población norteamericana se encontró cifras de colesterol medio de 241 mg/dl y una desv.st. de 45 mg/dl. Interesa probar si la población agrícola tiene mayor nivel de colesterol. Se estudió a 100 campesinos obteniendo una media de 249 mg/dl. Asumir un nivel de confianza del 95%. Ho: La media es menor o igual que 241 H1: La media es mayor que 241 Z <= 1,645 Z > 1,645 Z = (249 - 241) / (45 / 1001/2 ) = 1,77 Z se encuentra fuera de la región de aceptación ( Z <= 1,645 ) con un valor de p = 0,038 Luego: se rechaza Ho, los sectores campesinos tienen mayores niveles de colesterol. a_dat117/jsc ANÁLISIS DE DATOS MUESTRAS PROVENIENTES DE: Un Universo Dos Universos x1, s12 x1, s12 x2, s22 x3, s32 x2, s22 x4,, s42 a_dat111/jsc ANÁLISIS DE DATOS Diferencias de Medias Muestrales: Intervalo de Confianza: (X1 - X2) - K X1-X2 <= µ1 - µ2 <= (X1 - X2) + K X1-X2 donde: = n1 + n2 - 2 si >=32 K ==> Z 2X1-X2 = S21 / n1 + S22 / n2 si < 32 K ==> t 2X1-X2 = S2p ( 1/ n1 + 1 / n2) S2p = [ S21 (n1 - 1) + S22 (n2 - 1) ] / ( n1 + n2 - 2) a_dat112/jsc ANÁLISIS DE DATOS Diferencias de Medias Muestrales: Ejercicio: Se estudió el contenido de yodo en sangre en dos muestras de 20 personas cada una: en las mujeres se obtuvo una media = 5,9 con una desv.st. = 1,1 en los hombres se obtuvo una media = 6,8 con una desv.st. = 2,0 Si se considera un nivel de confianza del 97%, ¿existen diferencias significativas en los contenidos de yodo entre ambas poblaciones? = 20 + 20 - 2 = 38 => utilizar Z, reemplazando en la fórmula: 2X1-X2 = S21 / n1 + S22 / n2 2 / 20 + 2,02 / 20 = 0,51 1,1 ==> reemplazando en la fórmula del intervalo: (X1 - X2) - Z X1-X2 <= µ1 - µ2 <= (X1 - X2) + Z X1-X2 5,9 - 6,8 - 2,17x0,51 <= µ1 - µ2 <= 5,9 - 6,8 + 2,17x0,51 - 2,0 <= µ1 - µ2 <= 0,20 Dado que el intervalo incluye el valor nulo igual a cero, entonces se dice que no hay diferencias entre mujeres y hombres respecto al contenido de yodo en sangre. a_dat113/jsc ANÁLISIS DE DATOS Diferencias de Medias Muestrales: Ejercicio: Para estudiar si la presión sanguínea está relacionada con el tiempo de sangrado, 12 personas fueron sometidas a una presión en el brazo de 40 mm Hg. Se obtuvo un tiempo medio de sangrado de 2,192 seg. Con una desv .st. = 0,765. Se incluyó a un grupo control de 14 personas que no estuvieron expuestos a sobre presión, encontrándose una media = 1,407 y una desv.st. = 0,588. Construir un intervalo de confianza para la diferencia de las medias a un nivel de confianza del 95%. ¿existen diferencias significativas? = 12 + 14 - 2 = 24 => utilizar t, reemplazando en las fórmulas respectivas: S2p =0,7652(11) + 0,5882(13)/ 24 = 0,455; 2X1-X2 =0,455(1/12+1/14)=0,26 reemplazando en la fórmula del intervalo: (X1 - X2) - t X1-X2 <= µ1 - µ2 <= (X1 - X2) + t X1-X2 2,192 - 1,407 - 2,06x0,26 <= µ1 - µ2 <= 2,192 - 1,407 + 2,06x0,26 0,249 <= µ1 - µ2 <= 1,321 Dado que el intervalo no incluye el valor nulo igual a cero, entonces se dice que si hay diferencias significativas entre ambas situaciones evaluadas. a_dat114/jsc