Geometría 2. Curso 2007-08. Examen Final de Junio

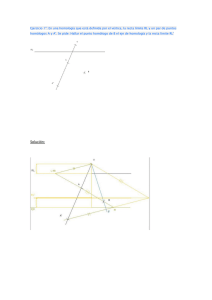
Geometría 2. Curso 2007-08. Examen Final de Junio
1. Teoría: Centros de un triángulo, recta de Euler.
2. Sea ABC un triángulo y A0 B 0 C 0 su triángulo medio. Si hP,λ es la homotecia de centro P y razón λ, calcular hC 0 ,3 ◦ hB, 23 ◦ hA, 21
3. Sea ABC un triángulo en el plano afín y f una afinidad tal que f (A) = B,
f (B) = C y f (C) = A.
a) Demostrar que f tiene exactamente un punto fijo.
b) Si las cevianas A ∨ A1 , B ∨ B1 , B ∨ B1 son concurrentes y f (A1 ) = B1 ,
f (B1 ) = C1 y f (C1 ) = A1 , demostrar que A1 B1 C1 es el triángulo medio de
ABC.
4. Sea F una familia finita de convexos del plano afín y [A, B] un segmento.
Si para cada 3 convexos de F existe una imagen trasladada del segmento contenida en los 3 convexos, demostrar que existe una imagen trasladada de [A, B]
contenida en todos los convexos de F.
5. Decidir cuales de las siguientes afirmaciones son verdaderas o falsas razonando las respuestas:
a) La composición de dos homologías generales con el mismo eje y distintos
centros es una homología.¿Puede ser una homología especial?. Interpretar el
resultado afinmente.
b) Dado un triángulo ABC en el plano afín siempre existe una proyectividad
que fija los vértices del triángulo y lleva su baricentro en un punto de la recta
del infinito.
c) Toda proyectividad fija al menos una recta.
d) Dado un cuadrilátero ABCD en el plano proyectivo, como en la figura,
los puntos A, C; E, H forman una cuaterna armónica.
1
6. Teoría: Teoremas de Pascal y Brianchon.
7. Teorema. En el plano proyectivo, si ABCDE es un pentágono circunscrito a una cónica propia, entonces las diagonales B ∨ D y C ∨ E y la recta que
une el vértice A con el punto de tangencia F en el lado opuesto son concurrentes.
a) Enunciar el teorema dual.
b) Enunciar la versión afín del teorema cuando E ∨ D se toma como recta
del infinito.
c) Si C es una cónica propia en el plano proyectivo y A es un punto que no
pertenece a C, demostrar que existe una homología con centro en A que deja
fija a la cónica.(Indicación: usar el concepto de polaridad).
8. a) Encontrar la ecuación de la parábola que pasa por los puntos P1 (0, 1),
P2 (0, 0) y P3 (3, 1) y cuyo eje es paralelo a la recta x + y = 1.
b) Clasificar proyectiva y afinmente, según los valores del parámetro a, la
cónica (1 + a)x20 − 2x0 x1 − x21 + x22 = 0.
Primer Parcial: Preguntas 1,2,3,4
Segundo Parcial: Preguntas 5,6,7,8
Toda la Asignatura: 3,5,6,8
Puntuación: 2.5 puntos cada pregunta.
Tiempo: 3 horas y media.
2