PDF (Parte 3)

Solución:
0.3 = 0.333... = 0.3 + 0.03 + 0.003+
3
3
+
" 10 102
1_
= 3 lim
+
3
_ y j _
3+
10 " " t?10 n
Co-!i , „ 1
30
1
.
-3 = j
r~-3 = —
3
=
9
3
_2
_ 1
10
10
73
EJERCICIOS
I). Demostrar que las siguientes series son todas divergentes.
3Ï"
a)I(k-l)
b) ¿ ( k 2 - k)
c) t { ¡
tTi
k-l
cYln^
tí U +
II). Demostrar que las siguientes series son todas convergentes y hallar el valor
de convergencia si es posible.
4
vl
a)
f t ( n + lXn + 2)
^ y*
d )
5(n
+
«
lXn + 2 X n + 3)
2n + l
n ( n + l) 2
2
^ f í
€)
»
{ ¿ V
n
V^ÊHzVn
X
j) I - ^ r r í
III). Escribir la fracción decimal periódica siguiente, como una serie y halle el
valor de convergencia de ésta.
a) 0.222...
b) 0.6161616...
d) 0.111...
e) 3.2323...
74
c) 0.832832...
V). Verifique:
oc
a) £ x
X
ac
n
* Zx"
si
W<1
si
=
w <1
De los ejemplos anteriores se puede argumentar que para decidir si una serie
dada es convergente o divergente, primero se tiene que determinar una
fórmula sencilla para su n-ésima suma parcial, pero no existe un método
general para lograrlo y es por ello que en las próximas secciones nos
•limitaremos a analizar si una serie dada converge o no, utilizando
procedimientos indirectos, esto es, sin el conocimiento explícito de una fórmula
concreta para la n-ésima suma parcial de Sn.
VI). Cuáles de los siguientes enunciados son falsos (justificándolo).
1. La serie Y —¡=
•==—
í((C
n
+
es divergente
(n + 5Xn + 6)J
75
es convergente.
VII). Hallar el valor de A tal que:
n=10v '
y
-
J
V r i
!
2. £ ( n + lXn + 2)
J f
i
.1=4
3-1
ti
Ì+A
V £ í ( n + l X n + 2) )
I ' i J +A
n - l ) - ItíW
2.6. PROPIEDADES
2.6.1. Si la serie ^ a n converge y an> 0 para todo n € N, entonces ]Ta 0 > 0.
ti* I
n*l
Demostración (ejercicio).
X
|
Ejemplo 1. La serie Y
>0
t í ( n + l)(n + 2)
Solución:
x
1
1
a. =
—
— > 0 Fpara todo n e N y Y
converge,
pues
5
(n + lXn + 2)
t í ( n + lXn + 2)
' F
s
n
=
f
1
_ y f
IY k + 2)
2ï
£¿ fí (í k + lXk
1
H= 1
2J
n+2
limS„ = IHao
lim
X
2
1
L_l
+ 2/
téí íVUk + 1 kV +
1
=
_yí_L__
¿i I v j+. 27
£fVk
1
k+1
^
n +=—
2 ' v Fpor ende,
00
1 ^ 1
1
1
= - entonces Y
= - > 0.
n + 2/ 2
t í ( n + lXn + 2) 2
f1
v2
J
luego Y
> 0.
t í ( n + lXn + 2)
2.6.2. Si las seríes £ a n y £ b 0 son convergentes y 0 < a n < bn para todo n s N
n=l
50
entonces ^T a n <
n=l
ti=l
3C
bn
n=l
Demostración (ejercicio). Obsérvese que se trata de series de términos
positivos, sin este requisito la conclusión es falsa.¿ puede el lector construir un
ejemplo ?.
77
co
oo
Ejemplo 1. Verificar que la
——
< T ] —3
n ^ n +5n + 6 j ^ n +3n + 2
Solución:
b
y
°
=
^ b i
y
a
=
°
;
1
y
1
^n2 +5n
. +. 6A ~£ í ( n¡ n+-L.2Xn
OVn+ 3)
-iy
L
¿?(n + 2Xn + 3)
_
f
(
-b°(ejercicloX
entonces
1
1
1
y
v^
/ J2
3 T, £~í•n- + 3 n + 6 t í ( n + 2)(n + 3)
_
1
<
1
1
_
¿?Vn + 2
1
- l ú . / y
(n + 3)j
1
1
1
Or
= -lim , ——— - T — - 1 =hmf
n->A(k + 3) k + 2; n-*«v3 n + 3J
1
1
-
™ l ¿ í ( k + 2)
2
k+3
1
y
3 "
2.6.3. La multiplicación de cada término por una constante diferente de cero,
no afecta el carácter de la convergencia o divergencia de la serie ( solo afecta el
valor de la serie si ésta converge), es decir;
Jí
»
i). Si X a » converge y c es una constante entonces X c ' a n converge
yZ
C
a
=C
n
n= l
Xan
n= l
ii). Si £ an diverge y c * O entonces ]T c • a„ diverge.
n=i
n-l
Demostración:
n
*
i) Sea S„ = y \ a t y como la serie Y a n converge, entonces limSn existe
n
n—>ao
30
y por tanto nlimc-S
y— asi esto es, la _serie Xcj "a>>
n = c- limS„ existe;
-*«
n
convergente..
n
78
es
ii). Como la serie Y an diverge entonces limtn = linaza,, no existe
t-i
JO
entonces limc-t n no existe y la serie X c ' a n diverge.
Ejemplo 1.
=«
La serie Y
00
|
f ]
=Y
(n + 3Vn + 2) tfVn + 2
1 ^ 1
= - (verej2.6.2.),
es
J
n + 3^ 3
convergente , entonces las serie Y —————— converge
5 v ademas
(n + 3)(n + 2)
'
5
'( 5
5 1
Af 1
O
5
— £íVn +z2
tT(n + 3)(n + 2)
—£?Vn + 2,
n + 37
n + 3^
oo
3
oo
Ejemplo 2. La sene
1 diverge entonces la serie
n=l
5 diverge .
n=l
30
ac
JC
2.6.4. Si las series X a n y X bn convergen entonces la serie X ( a
oo
oo
también convergen y además
oo
( a n ± b n ) = ^ an
n=l
± ^¡T b n .
n=l
n=l
Demostración:
30
Como las series X
X
a
n«l
n
y X ^ n convergen entonces
i» « i
ii
ii
limSn = n—kan
lim Y
a k y n—k
limTn = n—k-n
lim Y
b k existen, por consiguiente,
'
••••
1
a
Z„
"*
b
±X o = l™sn ± ü m T
mmmm
»—*cn
n—kar.
= n—fcOT
lim(Sn ±T„)
= lim\
fl—»30
A
x
= l m i X ( av k ± b k ) = X ( a D ± b n ) .
n-*® 7~T
,
79
\
a
X , ± Xbk
—
k=l
leal
/
'
»
1
»
1
Ejemplo 1. Como las series Y
,Y
convergen,
„IT n(n +1) 0=1 (n + 3Xn + 2)
entonces >
±
converge y
t í V n ( n + l) (n + 3Xn + 2)J
¿í—î—±
tíVn(n+l)
1
-1 = ¿ — ! — ± ¿
(n + 3Xn + 2>;
£?n(n+l)
Si las series Z a n y Z ^ «
2.6.5.
n«l
son
1
t í ( n + 3Xn + 2)
convergentes y si a yP son
números
n=l
reales, entonces por la propiedad 2.6.3,
»
X
ao
a
a
I(aa
n >' X P ' b»
B
son
convergentes y por la propiedad 2.6.4,
±pbn) = a-2a
B
±Plbn,
que constituye la linealidad de las series infinitas.
Ejemplo 1.
• x1 7T = X
La sene ]T —
t í n ( n + l) t í v n
1 7]
> =1y
77 = 3
n + lv
£?n(n + l)
luego la serie Y | — - — ± — — — ! es convergente y
oTÍvn(n + 1) n(n + \)J
l^?Vn(n+l)
i ^ ^n(n+r l)JH £ í n^( n +il) - „., n (30
n+l)
]
=4¿
± 3 0Y
= 4 + 30
tín(n+l)
£ í n ( n + l)
SO
son
convergentes,
Ejemplo 2. Las
series
"
Y
tí
flV
°°
— y X 7
V2J
"
4
r r son convergentes,
(n + 3Xn + 2)
00
" (lV
4
son convergentes. Por eso
luego las series Y 3 — y Y
t í \2J
t í ( n + 3Xn + 2)
Y <{ 3| — | ±
t í V2)
(n + 3Xn + 2)
j\3Íiy±
t í [ V2J
4
(n + 3Xn + 2)J
es convergente
y asi
5
J
1
l-3-ZÍlT±4-¿tíUJ
X
t í ( n + 3Xn + 2)
30
2.6.2. Si la serie £ a n converge y la serie £ b 0 diverge entonces
n-l
n-1
x
la serie X ( a n - ^n) diverge.
n-l
Demostración:
Argumentamos
por
contradicción.
Suponga
que
QO
^
j a )
converge, y sea b n - (a n + b n ) - a n entonces
la
serie
n=l
x
^
co
b n converge, puesto que las series ^ a
n=l
n=l
oo
n
y ^(a
n
+ b n ) convergen y
n=l
00
esto es una contradicción. Ya que por hipótesis ^ b n e s divergente. En
n=l
oo
consecuencia ^¡T (a n + b n ) diverge.
n=l
Ejemplo 1. La serie ¿ f — j diverge y la serie ¿ f - j
81
converge, entonces
- fi m Y
la serie ]>] —± diverge.
V3V
a=l Vn
1
Ejemplo 2. La serie
ri
i ^
" i
—+
diverge, ya que la serie ]T— diverge
n(n + l)y
n=i n
n=iVn
"
1
y la serie Y"
converge.
f \ n(n + l)
Notas:
00
i) Si la serie ^ ( a n ± b n ) es convergente, no se puede concluir que las series
n=l
oo
^
oo
an y ^
n=l
sean convergentes.
n=l
Ejemplo 1. La serie ¿ [ ( - 1 ) " - ( - l ) " ] es convergente, sin embargo la
n - l ••
X
serie ] T ( - l ) n es divergente.
n-l
oo
oo
îi). Si la series ^ T a n y ^T b n son divergentes entonces.
n=l
n=l
oo
las series
± b n ) puede ser convergente o divergente.
n=l
Ejemplo 1.
JO
x
00
Las series X1 -v X1
l
son
w=l
divergentes, y la serie
JU
divergente y la serie
(l -1) es convergente.
n= 1
82
+ l) =
es
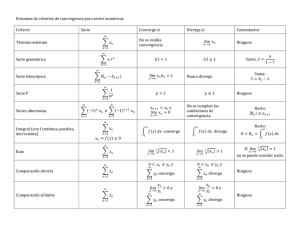
2.7. CRITERIOS DE CONVERGENCIA
Antes de emplear una serie infinita en posteriores situaciones u otros fines, se
debe analizar si es convergente o divergente. En teoría, la convergencia de una
sene se decide estudiando la convergencia de la sucesión de sumas parciales
(S„).
En pocos casos, como en las series geométricas y telescópicas, es fácil obtener
una expresión para Sn que nos sirva de apoyo para poder determinar la
convergencia de la sucesión (Sn), es decir, es factible evaluar el límite:
n
limSn = lim y ^
c
n—»oc
Sin embargo, en la práctica obtener una fórmula concreta para Sn deviene la
mayoría de las veces en un trabajo difícil o dispendioso. Por lo tanto se hace
necesario desarrollar reglas indirectas denominadas criterios de convergencia o
divergencia a luz del término general (an).
Los criterios con que se pretende analizar una sene de aquí en adelante se
referirán a una serie de términos positivos, salvo mención explícita de lo
contrario.
2.7.1. Criterio del término n-ésimo.
Este criterio resulta particularmente útil, para mostrar que una serie dada es
divergente, simplemente teniendo pleno conocimiento del limite del término
n-ésimo, veamos.
x
Si Y a .
nȒ
'
converge, entonces lim a n = O
n-»x
o en forma equivalente:
Si lima n * O jo lima n no existe) entonces la serie Y a , , es divergente.
83
Demostración:
n
Sea S n = 2_. a k ' a n-ésima suma parcial de la sene y sea S = lim S n .
t\
Dado que a ^ S n - SnA = (arH2+...+a,,) - (a 1 +a 2 +...+a n -i)
entonces lim a n = lim ( S n - S n _ ] ) = lim S n - lim S n _ i = S - S = 0.
n—>00
n—>oc
n—>00
n—>00
Nota: observe que el recíproco de este criterio no es cierto considérese el
1
* 1
contra-ejemplo clásico: lim — = 0 y la serie Y — diverge. Dicho de otro modo, la
n
tí n
oc
proposición:
si
lima 0 = O entonces Y a „ converge es FALSA!.
En
otras
n«l
x
palabras:
Si
lim a n = O e n t o n c e s Y a n
puede
ser
convergente
o
n=l
divergente!
Ejemplos.
1. La serie Y
diverge, pues lim
= 1*0
tí n+ 1
n +1
x
2. La serie Y n diverge, ya que lim n = +00
Véase este mismo ejemplo en página anterior en donde empleamos únicamente
hechos relativos a la serie geométrica.
3. La serie
diverge, pues l i m ^ l - — j
= e~3
n=o
y
(
j^-J diverge, pues lim^-J
f 5
4. La serie ^
n =o
3
84
= +00 * 0
oo
• V 1
1
5. La sene > — converse (por qué?), entonces lim — = O
oo
Z
n=l
1
1
converge,
entonces lim
=O
6
( n + l X n + 2)
n->oo(n+lXn + 2)
2.7.2. Criterio de acotación. Este criterio demanda un conocimiento
pormenorizado de las propiedades de las desigualdades de los números reales,
pues la acotación como se verá, involucra símbolos "<" (menor o igual que) o
">" (mayor o igual que), y dice lo siguiente:
00
Una sene ^ a n , con a n >O, para n e N, converge si y solo si su sucesión de
n=l
sumas parciales es acotada.
Demostración: S n = ai+a2+...+an puesto que an > O se tiene
Sn+i>Sn, ya que Sn+i = a1+a2+...+an+an+i>ai+a2+...+an = S n
es decir, (Sn) es una sucesión creciente y como es acotada entonces,
lim S n existe y la serie dada es convergente. Recíprocamente si, la serie
n—>oo
oo
^ a
n
converge, entonces para Sn = Y a t , se tiene que limSn existe y por
n-> c
tí
°
n=l
consiguiente la sucesión (Sn) es acotada.
oo
Ejemplo 1. Demuestre que ^ — es convergente.
n=l
0
1
1
1
1
1
1
eSolucion:
.
c = 1, + —
S„
+ —+ — +...+—< 1 + —+ —+...+1— - v= >1——2! 3! 4!
n!
2 2
2
HÍ2
85
0+1
1-
•2 = 21 2 - ^ | - 2 < 2
1luego O < S„ < 2, es decir, {Sn} es acotada y como {Sn} es creciente (ejercicio)
oo
entonces {S„} converge y así la serie
es convergente.
n=l
oo
Ejemplo 2. Mostrar que la serie ^
t i ^
2
es convergente.
"
Solucióo:
S „ = ¿ — J — r S ¿ - V = l - - V < 1,luego 0 S S . S 1 , por lo tanto
¿
¿
k=I (K + 1)1
(Sn) es acotada y como (S„) es creciente (ejercicio), entonces (S„) converge y la
1
serie dada X
777 converge.
oTi (n + l)2
00
Ejemplo 3. La sene
n es divergente.
n=l
Solución:
Sn = ¿ k =
es una sucesión no acotada y creciente, por
k«l
y.
ende la serie X
n
diverge.
n=l
00
Ejemplo 4. La serie Z Í - 1 ) " diverge,
a
Pesar
de
<lue
la
n-ésima suma parcial
n=l
S n es acotada, (pero no es creciente, ni decreciente). En este ejemplo el criterio
no es aplicable, pues an =(-1 ) n , es positivo para n par y negativo para n impar.
2.7.3. Criterio del resto. Una serie X a „ converge si y solo si cualquiera de
n=l
x
sus restos converge y s i S = X
n
a
0=1
n;
S
n
=
oo
a
R
X ky o
k=l
86
=
XX
k-o+í
entonces
ce
oo
S = S n + R n y además £ a k = 2 > n + k = S - ( a , + a 2 +...+a n )
k=n+I
k=l
D
00
Demostración: Sea S n = Z a k > ' a n-ésima suma parcial de £ a n y
k-1
sea
n=l
^k la
suma de los k términos suprimidos y L„_k la suma de los términos de la serie
que participan en la suma S„ pero no en la Ck, entonces, S„ = Ck+L„-k, donde Ck
es una constante que no depende de n, entonces lim S n existe, si y
n-*°o
solo si lim L
. existe,
n—>co n - k
Nota: De esta propiedad se puede concluir que la supresión o adición de un
número finito de términos no afecta el carácter de la convergencia o
divergencia de una serie (solo afecta el valor de convergencia, en caso de ser
convergente la serie).
x
1
1
=
Ejemplo 1. La sene ^ ( n + SXn + 2) 3" Y
^
1
ntTo(n
«
P
°r
Cnde
'
i
es convergente, pues es un resto de la serie
+ 2 X n + 3)
i
que es convergente.
z—-—
t ? ( n + 2Xn + 3)
Ejemplo 2.La serie Z í ~ j ^ convergente, ya que es un resto de la serie
o=IO
1 "
Z ( ~ I que es convergente.
Ml
Ejemplo 3. La serie
x
Z
n-l
1
-
n
n=ion
es divergente, ya que es un resto de la serie
Q u e es divergente,
87
r
"
£?( n + 2Xn + 3)
£ ( n + 2Xn + 3)
i _ f _ L JL _ L ) = i
3 l l 2 + 20 + 30y 6
Ejemplo 5.
Las
convergencia, (porqué)
30
1
<
„TÍ (n + lXn + 2)
i
n
siguientes
J
O
series
t
30
f,(n + 3Xn + 4)
tienen
el
1
S ( n + 2Xn + 3)
mismo
JO
valor
de
1
ntf0(n-8Xn-7)
l ^ l
V- l
1
b ) Y — = y — = y — = y
n-10
/ jL
/ j -»n-2
/ i -^n+1 / J Z-y
n=0
n=2 Z
n=—1 L
n=10
2.7.4. Criterio de comparación directa. Para tener éxito en la aplicación de
esta criterio se requiere de cierta habilidad y experiencia en el manejo de
desigualdades (ver apéndice), y de ciertos mecanismos que de una u otra forma
bien aplicados sirven para decidir si el criterio se puede aplicar o no; y este
criterio dice lo siguiente:
Suponga que las series ][]an y £ b n son series de términos positivos entonces:
n=l
i) Si ]!T
n=l
n=l
converge y an < bn para todo n e N entonces la serie
X
converge.
n=l
ac
ii) Si la serie ]Tb n diverge y bn < a n para todo n e N entonces la serie
serie ]Ta n diverge.
Demostración:
Sea S = a 1 +a 2 +...+a n y T n = bi+b2+...+bn, las sumas parciales n-ésimas de las
senes n
88
ao
S
n=l
ao
a
a
y Z ^ a respectivamente:
n=I
i) Como a„< bn para todo n e N entonces, S n = ai+a2+...+an < b1+b2+...+bn= T„;
00
es decir, S n < T n y como £ b n converge, entonces limT
n existe, es decir,(T n )
n=l
°->00
es acotada y además creciente, de aquí se concluye que (Sn) también es
ao
acotada, y creciente, luego lim Sn existe y la serie Yúrn converge.
n*= 1
ii) Como b„< a„ para todo n e N entonces Tn < s„ y
ac
limTn = +oo (ya que ]T bn diverge), se concluye que
n=I
oc
lim S n = +oo y la serie £ a n es divergente.
I1-+00
n=i
Nota: Hemos agregado una demostración para la proposición ii) en aras de la
claridad, pero es innecesaria, toda vez que ambas proposiciones son
lógicamente equivalentes.
Ejemplo 1.
2
1
—<
n +5n + 8 > n + 5n + 6, para todo n e N , entonces:—;
n ' + S n + S n~+5n + 6
=
x
l
1
—
Y como la serie Y
= 1- (converge) se inf iere que
(n + 2Xn + 3)
t ? ( n + 2Xn + 3) 3
la otra serie converge y además
00
1
00
1
00
£
i
<£
=¿
2
2
n =m +5n + 8
n =in +5n + 6
n=i(n + 2Xn + 3)
X
]
Ejemplo 2. Mostrar que la serie £ —
es convergente.
n=i(n" +5n + 5)en
50
l
1
1
1® 1
Solución: Y
—
-n ;' —2 ;— n _
< — -n como -- Y —a es
t — i . 52
n
o
n -e +5n-e +5-e
5-e
->n=oe
0=i(n +5n + 5)e
89
4
convergente (ejercicio), se concluye q u e £
n=o
- es convergente
(n* +5n + 5)e
. \ p l n ( n + 2)
Ejemplo 3. mostrar que la sene
es divergente.
n=2
^
Solución:
ln(n + 2) 1 , ,
ln(n + 2) > 1 si n e N , n > 1, entonces —
> — y dado que la sene
n
n
1
.
. ^ ln(n + 2)
diverge, entonces la sene ¿^
diverge.
n
n
1
Ejemplo 4. Mostrar que la serie £
es divergente.
n=3lnn
Solución:
1 1
" 1
ln n < n, n e N, entonces ; — > — y como la serie Y — diverge, se establece
lnn n
n=3n
® 1
que la serie Y - — diverge.
tí lnn
1 A
diverge.
Ejemplo 5. Mostrar que la sene £ I n l + i
n=2 v ¡sen n\J
Solución: sen nj < 1 ó
Ì
1
1
1
> 1, luego 1 +-—'—> 2, yin' i1 + T
7 > ln2
sen nj
¡sen n
V |sen n \J
1
\
diverge.
y como la sene de ]>]ln2 diverge, entonces ^ l n 1 +
V ¡sen riu
n=2
n*2
x
f n + 2Y 1
Ejemplo 6. Mostrar que la serie £
) • —- es convergente.
n=2^ n + 3/ 3
n+2
,
.
( n + 2^i 1 ^ 1
Solución:
< 1, para todo n e N , luego i
•— < — y como
n+3
Vn + 3 ^ 3 3
^ 1
•• x
.
n + 2^1 1
la s e r i e ? —
converge (ejercicio), entonces la sene > }
converge.
tt
tí3
t ^ n + 3/ 3
90
2.7.5. Criterio de la integral. Este criterio es de máxima importancia, pues
de un lado nos proporciona numerosos ejemplos de series convergentes y
divergentes y de otro lado puede ser efectivo para analizar la divergencia o
convergencia de una serie siempre y cuando se satisfagan las hipótesis
respectivas y la integral impropia que resulte sea fácil de realizar.
El criterio afirma lo siguiente:
Teorema
Sea f(x) una función definida en el intervalo [l,+co) que satisface a la
condición:
i)í(x)>0 para todo xe[l,+<x); (positividad).
ii) limf(x) = f ( a ) para todo a e [ l , + <x); (continuidad).
n-»«
iii) Si a<b entonces f(a)>f(b); (decrecimiento).
ac
oe
Entonces, la serie £ f ( n ) = £ a n converge si y solo si la integral impropia
n=l
n=l
j ^ f í x ^ i x converge. Es claro que todo depende de la dificultad del análisis de
la integral impropia
Demostración:
Sea a n = f(n); para n= 1,2,3,... si n < x < n+1 se tiene que f(n) > i{x) > f ( n + l ) ,
( f e s decreciente), luego:
91
f(n) = J7(n)dx > £f(x)dx > Jf(n+ l)dx = f(n+1) o sea que
4-1
in
OC
00 /Q-¥ 1
n>^
> Jf(x)dx > an+1 y de esta suerte, /^a
n=l
jf(x)dx
n=l
= Jf(x)dx> ^an+I; luego si ^ an converge, entonces jff(x)dx
n=l
n=l
n=I
= Jf(x)dx converge y si
diverge, entonces ^ jjf(x)dx
n=l
n=l
= Jf(x)dx diverge.
M
Ejemplo 1. ( Básico ). La serie-p,
n=l
1
n
<xmveT
B e si p > 1 y diverge si p < 1.
Solución :
i) Si p > l , f(x)=—r es continua, positiva y decreciente en
x
r
En efecto, f'(x) = -px ^ i = -—177p+1 < 0. Ahora, la integral
l-p
p
í — =o-moJi
limí x db-»°e
x = lim
>
1-p
Jl
X
dx
x
.
b;-p
= lim
b—>qov i - p )
• v- 1
n=i
i
i-P
esto es Ir —P converge, y la sene 2 _ , ~ Pc o n v e r S e
n
1 1
ii) Si p< 1; entonces np < n, lo que implica que — > — y como la serie
n
n
1
^ 1
/ — diverge, entonces la serie /diverge
para p < 1
(criterio de comparación).
92
Ejemplo 2.
Las series /
n=l
00
—; /
11
n=l
n
2
j
— . Son convergentes y las senes
n=l
11
—¡—
n=l
n
3
00
/ —¡=; 2 , s
t f V n t f n/?
o
n
divergentes.
30
Ejemplo 3. La serie
^
B
ne"
n« i
es convergente.
Solución :
S e a f ( x ) = xe~v , se tiene que f ' ( x ) = e' K • l - 2 x 2 - e ~ x = e ^ ( l - 2 x 2 ) < 0
si x > 1, entonces f es decreciente. Además f es positiva y continua en [l,+°o) y
como la integralJi xe~x dxb-»oo=i lim xe_x~b-»dx 2= lim- —
e
2e
f
x
:
f b
•>
J
1
21 b
1
1 1
= —,converge
®
2
se concluye que la serie ]Tne
es convergente.
ii=2
30
* e s convergente.
Ejemplo 4. La serie
n=2
Solución 1: Seaf(x) = e
f(x) es continua, positiva y decreciente en [1,+QC)
b
x
(ejercicio) y como la integral "2
Pe~*dx = limf
l'2! = e " ,
b—*oo J2e~ dx = lim-e~*
b-+3o
00
converge entonces la serie ^ e * converge.
n=2
Solución 2 : Tenemos una serie geométrica de razón r = - < l
e
- n2 e s
Ejemplo 5. La serie
convergente.
a=l e
Solución:
93
Sea f(x) =
f es continua, positiva y decreciente en [2,+co) (ejercicio),
ex
entonces el criterio de la integral se aplica al resto
n=2 e
00
®x2
n2
Como la integral f2° — d x converge (ejercicio),la serie
converge y la
e
n=2 e
x n2
serie
converge ( criterio del resto).
e
2.7.6. Criterio asintotico. Sean (a n ), (b„) dos sucesiones de términos
positivos tales que a„ « bn, es decir:
í
a
]
»
®
lim— = 1 o mas generalmente l i m — = A
entonces las series Y a B, Y b B,
x
V
— b„
)
„=, „=..
a
n
o ambas convergen o ambas divergen.
Demostración :
a
lim—= 1 significa que para todo £>0 existe N > 0 N - N(e) (N depende
I
a
\an
o'
de e), tal que si n > M, entonces ¡— - 1 < £ O -£<—-[<£,
K
a. .
1
. 1 a
1 .
. . 1 _a„ 3
—< 1 + e. si s — —, entonces 1 - - <n -f-<- + 1; es decir — < t 2 - <-, luego
bn
2
2 bn 2
2 bn 2
1
am y
a
3
rr
r 2
l a
De — <
b
se inf iere que ~
< a n y por el criterio de la comparación
=0
* (j
directa ; si X a „ converge, e n t o n c e s c o n v e r g e y de aquí
»
b n converge
n=í
94
30
si£b
30
n
diverge, entonces ^
n=l
a n diverge.
n=l
a
3
3
De — < —, se tiene, a n < — b B , y si
bn converge, de nuevo, por el criterio
bn 2
2
D=i
x
x
3
de comparación ]Ta n converge y si ]Ta n diverge, entonces^]—b n diverge
00
n=l
D— L
N=l
30
y
diverge.
n=l
Para facilitar la aplicación del criterio asintótico, se usan algunos principios
informales, tales como el despreciar constantes sumadas o restadas en la
fórmula del término n-ésimo an. Y si aparecen polinomios en n como factores
en ocasiones suprimir todas las potencias de n-exeptuando la mayor en cada
factor- favorece simplificar el análisis sin afectar el carácter de la convergencia
o divergencia de la serie ;obviamente cada paso exigen su propia verificación;
» Uln + 2 + n + 2jln 4 + n 2 )
La serie ]Ta„ =
—j—a ^ — ^ — j r — - se comporta como la serie
n=l
a=l
(2°+5)(3n7+n2)
®
® ( n )í n )
°°
1
2 > » = Z 7 7 ¡ w r 7 Y = E ^ - r Se puede probar
n=i
n=i |2 II 3n I
n = i 2 3n
a
que a a « b a , es decir, lim — = 1.
n-^-x V)
n
Ejemplo 1. Mostrar que la serie ¿ — 7 — y — es convergente.
„.i n + n +1
Solución:
95
n+2
n
n =—
r~:%-T
n + n +1 n
a
y como la serie ^
=
1
-T
n
= b
n' y
bn =
n=l
.. a n
n4+2n3
lun — = hm — — —
b n « ^ n + n +1
a
converge, entonces la serie
n=l
11
x
n+2
Z
—
converge.
=i n + n +1
n
Ejemplo 2.
• v^V n(n + l)
Mostrar que la sene ¿^
; — - converge.
n=i
2"
Solución:
Vn(n+1)
Vñ7
n
a
. . .
«
= —a = b n , ya que Iim —n = 1 (ejercicio) y como la
a
a
2
2
2
n-»«bn
x
serie
converge (criterio de la integral), entonces la serie
n=i ^
aQ =
Z
'JÜ
Vn(n+1)
r
o=l
converge.
Nota: No siempre la convergencia o divergencia de una serie dada se puede
analizar por cualquier criterio, en algunas oportunidades los criterios fallan en
el sentido de que las hipótesis correspondientes no se satisfacen, en otras son
muy difíciles de aplicar, y hay que saber muy bien el criterio a utilizar, como se
puede observar con el siguiente ejemplo.
Ejemplo 3. Mostrar que la serie ¿ —
diverge
n=i 3n +5n + 2
Solución : a) El criterio de término n-ésimo no es susceptible de aplicar o
mejor no conduce a mayor información, ya que :
iim
n
+1
_ o , y la serie en cuestión puede ser convergente o divergente.
3n + 5n + 2
:
b) Con el criterio de la comparación directa, hay que buscar una serie menor
que sea divergente, y ello es un poco difícil aquí.
96
c) Para este ejemplo es fácil aplicar el criterio asintotico.
n+1
n
2
3n + 5n + 2
3n
i
2
,
. a
.
= b n , ya que lim —n = 1, y como la sene
3n
b
X
30
X
^
^
/
— diverge, se tiene que la serie ) a = / —
diverge.
,
3n
f
f
3n"
+
5n
+
2
11= 1
n= 1
n= 1
M
1
Sin embargo este criterio sugiere la comparación con la serie X — que es
n=i 3n
divergente.
La desigualdad
n+
*
> — , no es correcta (¿por que'?), pero
3n + 5n + 2 3n
2
1
„
A 1 ..
,
.
n+ 1
—2¿
> — si es correcta para n > 2, y como ¿ j — diverge, la sene
3n +5n + 2 4n
*
n=2 n
a>
J
®
1
Y — diverge y asi Y — diverge, lo que implica que la serie
t í 4n
n=i 4n
—T——
diverge por el criterio de comparado' n
o=i 3n" +5n + 2
2.7.7. Criterio de paso al límite (generalización del criterio asintotico)
Este cnterio es uno de los mas recurrentes en la aplicación, y dice :
30
JO
n=i
o=l
Sean X a n ' X
dos series de términos positivos, de las cuales se sabe que
a„
Y bn converge o diverge y sea lim — = L entonces :
0=1
i) Si L*0 ; ambas series convergen o ambas series divergen.
x
x
converge entonces X a n
ii) SiL=Oy
n=l
o=l
97
converge.
iii) Si L=+<x y ^ b
t
diverge entonces
a=i
diverge.
n=l
Demostración :
q
i) Sea L>0, como lim—
= L, entonces para todo e > 0 existe N > 0
¡1—»ce ^
I
tal que si n > N entonces a — - L < 8, es decir, L - £ < — < L + e.
bn
bn
L
L a
L
L a
3
Si 8 = —, entonces L
< — < L + —, vde aqui — < — < —L.lueso
2
2 b.
2
2 b
2
3
1
para n > N , a n < - L b n y - L b „ < a t
n
ao
3
Si ]Tb n converge entonces ]Tb n converge y asi ]T —bn converge,
a=l
n=N
n=N
2
00
Luego por el criterio de comparación directa ^
a n converge y por el
n=N
00
criterio del resto
converge.
n=l
L
"
Además como —bn < a„, la divergencia de
bn diverge, implica la
2
_N
n
00
divergencia de £ a n , y asi /
a n diverge.
n=l
Como ejercicio demostrar los demás casos.
GO
• lnn
Ejemplo 1. Analizar la convergencia o divergencia de la serie ^jT
n=2T n
98
00
Solución: Sea la serie Y
Inn
lnn
con a n = —y Para aplicar el criterio 2.7.6. se
n=2n
n
oo
escoge una serie ^ b n , de la cual se conoce de antemano que es convergente
n=2
o divergente; seguidamente se calcula el lim — y se observa si algunos de
n-»oo b n
los tres enunciados dados en el criterio se cumple.
En caso de que ninguno de los enunciados se cumplan se procura escoger
adecuadamente una nueva serie y se repite el proceso.
Para este caso escojamos una serie convergente cuyo término n-ésimono
difiera sustancialmente de a„. Por ejemplo:
lnn
¿ ~ T = ¿ b n calculemos: lim— = lim-^— = n-*oc
Iimlnn = +oo.
n=2 n
b„
1
—
2
n
De los tres enunciados del criterio, cuando lim— = +<x¡, observemos que
CP
solo se puede aplicar cuando]Tb n es divergente y aquí fallamos ya que la serie
n«2
00
^ b n es convergente. Continuemos. Escojamos otra serie por ejemplo
n=2
oo ^
Z
_
- q u e es divergente y
lim— = lim-^—= l i m - ^ - = o.(L'Hopital);
"
|J
n-»«e K
o
n-+a¡ 1
a-*cc r\
*
00
nuevamente el criterio falla ya que se requiere que
b n sea convergente y en
n=2
este caso, la serie escogida es divergente..
99
Insistamos una vez mas.
Escojamos la serie
]JTbn
n-2
-5-que es convergente,. Ahora veamos:
n*2 fl 2
lnn
lim ~ J L = lim
n->oobn
— = lim —r~
= 0 (ejercicio),
l
1
n—>ec
n->oo
Á
n
3/
n 2
y en esta oportunidad observamos que el criterio si se puede aplicar, pues la
serie
g
Y b = y —— es convergente y lim — = 0, implica que la serie
"
%
n-tl hn
n=2
n=2 n 2
OC
oc
|
v ^ In n
Z
a „ = 2l» —~ es conver8ente
n=2
n=2
11
Ejemplo 2.
00
7,
—2
n=l
n
es divergente.
+ l
Solución:
^ — = X a n Observemos que la serie en eosideración se comporta
Sea
n*l n
+ 1
n.l
100
2n
00
como ^ ~ T ~ ^ — = ^ b n que diverge y Iim — = lim n
n—» qo ho
n-»oo
n=t n
n= 1 0
n=l
+ 1
2
n
2n2
= lim
= 1 * 0 , entonces
— 2 ( n 2 + l)
se deduce
de ta divergenci
a de la serie Y b
6
*
Xa«
la divergencia de la serie
00
Ejemplo 3. Demostrar que la serie ^
— es convergente.
n=l3
Solución:
00
La comparamos con la serie
^
00
— = ^ b n que es convergente y
n=l
n=l
3
n
a
•J"
calculemos, lim — = lim
= lim n = +oo
tl-»ao b
n-+=o 1 n-+oo
3°
entonces el criterio no se puede aplicar y la serie dada puede ser convergente o
divergente. Se necesita escoger adecuadamente otra serie o aplicar otro criterio.
00
Tomemos la serie /
^
— que es convergente y calculemos,
n^l
n
a
i»
n
i
^ ^
lim— = l i m — = lim= lim
= 0,yj en consecueciala serieY—o
n—o b
1 » - " / 3 Y »-M0/3V /^N
tí 3
V
v¿J
v.2y
converge
00
n3
Ejemplo 4. Analizar la convergencia o divergencia de la serie Y —
t í n!
Solución:
101
Tomemos Y— = Y V
y sea Ybn
0 = 5 n!
O=I
n +4)!
Q=5
y calculemos,
= Y— que es convergente
n = 5 n!
(n + 4) ]
3
a
(ri + 4)!
(n + 4) 3
^
JS, n
lim — = lim-——— = nhmco7
,,
., —r-,
r = 0 por lotanto > —
n-=°ba
J_
-* (n+l)(n + 2)(n +3}(n + 4)
n=5 n!
n!
converge, y la sene dada converge.
co
2.7.8. Criterio de Pringstheim. Sea
a n , una sene de términos positivos,
n=l
tal que lim n p a n = A entonces:
00
i) S i p > l y A e s
finito, entonces la serie ^ a
n=l
n
converge.
oo
ii) Si p<l y A * O (A puede ser infinito) entonces la serie
diverge.
n=l
Demostración. Ejercicio
En esencia, se toma como sene de comparación la p-serie ^ n p .
n=l
oo
Ejemplo 1. La serie
Solución:
^ — e s divergente.
Jim n p x — — = 1 * 0 , s i p = l.
n^oo
+1
n
oo
Ejemplo 2. La serie / - 7 = es divergente.
' Vn +1
n=l
^ .
Solucion:
nplnn
1
hm - ,—:— = +00, si p = —.
n—><xi Vn + 1
2
102
°°
Ejemplo 3. La serie ^
lnn
""
converge.
n=¿
Solución:
lim
n->oo
= 0, si p = —.
n
¿
+3
Ejemplo 4. La serie ^ T e
n
.3
converge.
n=l
Solución: lim n p • e
n—>30
3
= 0, si p = 3.
00
2.7.9. Criterio de la razón. Sea
una serie de términos positivos y sea
n=l
lim—1— = L
n-íoo
a
n
oo
i) SiL<l entonces la serie ^
a n converge.
n=l
oo
ii) Si L>1, entonces la serie ^ a
n
diverge.
n=l
oo
iii) Si L=l. El cnterio no decide, luego la serie
puede ser convergente
n=l
o divergente.
Demostración:
*i) Si L<1, sea R un número real tal que L < R < l y s = R - L > 0 ,
a
Como n—»oo
lim—1^— = L, para todo e > O existe N > O tal que
¡ ^ L - L < s, n > N; por tanto
i a.
a
< L + s, si n > N.
103
Si n toma sucesivamente los valores N, N+l,N+2,... de
a
n + l < R se tiene:
a
n
a N+l < R a N
a
a
N+2
N+3
<Ra
<R a
N+l
N+2
2
<R~*a
<R
J
N
a
N
M
a N + M <...<R
a
N
, para todo M e Z
, luego
9
a
N+l
+a
N+2
+...+a
y asi la sene a
;
N+M
<Ra
N
+R
a
N
M
+...+R -a
N
+...
+ a N , +... converge (criterio de comparación), ya que la
serie R-av+R~ • a +... converge; pues es una serie geométrica con 0 < R < 1 y
aN es un número fijo y positivo.
cc
La serie ^ T a ^
oo
M
difiere de la serie ^ a
M=1
n=l
oo
términos,luego la serie
^ a n converge.
n=l
ii) (ejercicio).
iii) Las series
104
n
. solamente en los N primeros
XJ X |
'
muestran que cuando L = 1 debe aplicarse otro criterio, ya que:
n=i n n=i rT
1
(i) para ¿ I ; ^
=ü f i =
y l i m ^ - = I iaom - ^
=i
n
a
i
n
+
1
a„
*-* n + l
n
n
n
1
¿ i
-m
^ ,
an
1 ^ 0 1 = y
_1_
(n+1)
2
n
00
En ambos ejemplos L = 1, pero
an
|
—
„lim
n _
«— (n +-1)"
X
1
diverge y ]>]— converge.
n=i n
n=1
El criterio de la razón es a menudo efectivo cuando los términos de las series
contienen factoriales, o expresiones con potencias n-ésimas o combinaciones
de estas, como se mostrará en los ejemplos siguientes.
00
Ejemplo 1. La serie
—J
converge.
n=l
-j-^n+1
c i
i an+t
Solution 1. -üx¿- =
a
f2\n
=
n
o
v3/
3
f2^
n
2
a ,i
2 ,
= — ; como hm nn + l = —<1,
3
n->oo a n
oo
el criterio de la razón prueba que la sene
n=l
Solución 2. Se trata de una serie geométrica.
00
Ejemplo 2. La serie
j
— converge.
n=0 n '
105
]
^
converge.
3
4
Solución:
h± =
an
=
J_
n!
_ L y lim
n!(n+l) n + 1 « « a,
=
=
(n+l)!
£ 1
1
= lim
= 0 < l,y asi la serie Y — converge.
5
— n+l
¿n!
00
Ejemplo 3. La serie >
Solución:
——converse
2
< _JL. < JL
4 - 2 + 3 4-2
2
y
aplicando el criterio de la razón a la
00
— , obtenemos:
a„+1
a
=
n
2nn+1
a (
n+l
1 ,
+ l _ 2 " ( n + l ) - n + l y [, _JL_L
= - < 1.
m
= |lm
JL
2 (n)
2n
a^
2n
2
2"
30
entonces la serie
converge y por el criterio de comparación la
n=i
serie ^
2
——"—- converge igualmente.
00
2.7.10. Criterio de la raíz (Cauchy). Sea
. .
positivos, y
n=l
i/
limn"=L
/I—»00
a n una serie de términos
"
00
i) S i L < l , entonces la serie ^
a n converge.
n=l
106
00
ii) Si L>1, entonces la serie ^ a
n
diverge.
n=l
00
iii) Si L=1 la serie ^ a n puede converger o diverge.
n=l
Demostración:
i) Sea L<1, como lima'" = L, para todo e > 0 existe N > 0
11—* oo
tal que si n> N entonces \Qn" - L < s, es decir, q " < L + e. y
Qn < (L + e)n. Como e>0,se
00
escoge e tal que L + e < \, luego
00
a n < £ ( L + £) n , que es convergente, ya que L + e < 1 y por
n=N
n=N
00
el criterio de comparación la serie
converge, de modo que la serie
n=N
00
y ' a n converge.
n=l
ii) (ejercicio).
00
iii) Las series /
n=l
(\y» V
pues lim —
1 °° 1
—, V - T , muestran que el criterio no decide, cuando L = 1
n=l n
(, 1. ^. i n
= 1 y lim —
" J
=1 (ejercicio) y > — diverge,
«^ 1
/ — converge.
00
1
Ejemplo 1. La serie ^jT— converge.
n=l
T
107
1/
n
Solución: lim £
n->oo
n
r
=
Vn
lim
n->ooV2n^
oo
1
1
= j- < 1, luego la serie V — converge.
2
' ' -) n
n=l
n
y diverge.
Ejemplo 2. La serie
~
n=ii n
Solución:
f ry n
lim o
n
2
^ 2n
lim —— = 2 > 1, entonces la serie > —diverge.
n" n
r r n"
= lim
n—»oc
n—»ce
Ejemplo 3. La serie / J 1 + —j
Solución: lim
decide,
lim
ann = n->oo
luego
n
hay
que
diverge
1/"
n /n
1+
lim 1 + — ] = 1 y el criterio no
n — n ^
n.
aplicar
otro
criterio.
Observe
que
lim a n = lim í l1++ — = e * 0, luego por el criterio del término n-ésimo
n/
n—>cc
n—»ccrA
oo
n
(
la serie ^ 1 + — diverge,
n^
n=l
30
Ejemplo 4. La serie ^
2 n + J3 n
~
converge.
5
n=l
Solución 1.
]T
n=l
1/
lim
(DI
n
2" 4-3"
5"
+
ShJ £UJ
_ 2 < 1 y lim" 3 V l "
3
-J
= - < 1, ambas senes convergen y así la
5
00 2 n + 3 n
sene
y
n=l
ycomo
5n
converge.
108
Solución 2. Estamos en presencia de dos series geométricas. En caso en que el
criterio de la razón o raíz no deciden, se puede intentar con el criterio de
Raabe, a saber:
oo
2.7.11. Criterio de Raabe. Sea ^ a n una serie de términos positivos y
r
calculemos, lim n l - £ s ± l
n-»oo
n=l
\
v
an
oo
i) Si R > 1, la serie ^ a
n
J
= R entonces:
converge.
n=l
oo
ii) Si R < 1, la serie ^ a
n
diverge.
n=l
Demostración:
r
i) Si n
\
|
V
a
n+l
an
f
a
> a > 1, entonces 1 - n+1 > —,
es decir, 1. —a - > n + i
n a
J
v
an y n
luego ^ S ± L < 1 - n
a
ó n-a n+1 < ( n - l ) a n - ß • a n ; ß = (a - 1 ) > 0; y así
( n - l ) a n - n - a n + I > ß - a a >0.
oo
La
serie
telescópica
^
oo
c n = ^ T ((n - 1 )a n - n• a n + j )
es una
serie
n=l
n=l
convergente si (an) converge, luego por el criterio de comparación la serie
co
00
ß • a n converge y de esta suerte la serie ^ a n es convergente.
n=l
n=l
ii) Se demuestra en forma similar.
109
00
1
Ejemplo 1. La sene >
=
^
2.4.6..,(2n)
n=l
n=l
1.3.5...(2n-l).(2n + l)
2.4.6...2n.(2n + 2)
Solución: i) 'n+I
2.4.6..,2n
1.3.5...(2n-1)
2n + l
-Juego
2n +
1 y el criterio del cociente no decide.
ti—« "'n + 2
n—»» "nn
q
diverge.
"
lim n| 1 - 2 n + 1 l = lim — - — = — < 1,
n-»® V 2n + 2/ n-^® 2n + 2 2
ii) lim n 1- IH-i
V a nn )
JU
entonces la serie ^
a n diverge.
CO
Ejemplo 2. La serie
1.3.5...2n - 1
2.4.6...2n
^
n=l
Solución: i) ^iL
ii) lim n-| 1
f
lim nII-»«) v
12
=[
" Ü„ZL•Li
a
n
converge.
+
) , v lim — ^ = 1 (falla criterio cociente)
2n + 2/
a„
lim n- ,
n—»oo
.
(2n+1)3i
(2n + 2 y j
8n3 +12n 2 +6n + P
8n3 +24n 2 +24n + 8y
= — > 1, luego la serie
-v
H
^
n=l
= lim nn—*oo
1.35.2n-1
2.4.6.. 2 n
110
'
12n2 + 18n+ 7
^
^8n3 +24n 2 +24n + 8y
converge.