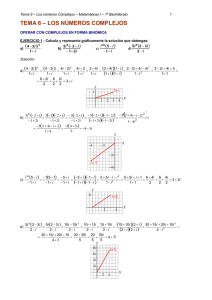
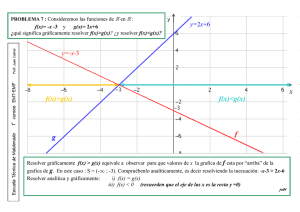
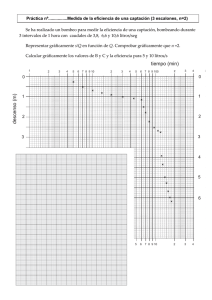
Evaluación de Números Complejos Tema A 1. Efectuar la operación y expresar el resultado en forma binómica a+bi, con a y b números reales: a) 5 6 i 7 2 i b) 2i 2i c) 3 16 7 9 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 5 i b) 2i c) e j d) 2 3i 4 3. ¿Cual es el número complejo cuya parte real coincide con la parte imaginaria y tiene módulo 2? 4. Calcular z1 .z 2 y z1 y expresar el resultado de la operación en forma polar y en forma binómica. z2 a) z1 1 i z2 1 i b) z1 3 i z2 2 i 5. Hallar el complejo z en la ecuación 8 7i z 7 5i 3z 5i 7 (2i 3) Evaluación de Números Complejos Tema B 1. Efectuar la operación y expresar el resultado en forma binómica a+bi, con a y b números reales: a) 3 6 i 5 2 i b) 4i 4i c) 5 1 7 4 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 7 3i b) 5i c) e j 2 5 d) 4 3i 3. ¿Cual es el número complejo cuya parte real coincide con la parte imaginaria y tiene módulo 5? 4. Calcular z1 .z 2 y z1 y expresar el resultado de la operación en forma polar y en forma binómica. z2 a) z1 1 i b) z1 3i z2 1 i z 2 5 i 5. Hallar el complejo z en la ecuación 8i 7 z 7i 5 3z 3 7 (2 3i) Evaluación de Números Complejos Tema A 1. Efectuar la operación y expresar el resultado en forma binómica a+bi, con a y b números reales: a) 5 6 i 7 2 i b) 2i 2i c) 3 16 7 9 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 5 i b) 2i c) e j d) 2 3i 4 3. ¿Cual es el número complejo cuya parte real coincide con la parte imaginaria y tiene módulo 2? 4. Calcular z1 .z 2 y z1 y expresar el resultado de la operación en forma polar y en forma binómica. z2 a) z1 1 i z2 1 i b) z1 3 i z2 2 i 5. Hallar el complejo z en la ecuación 8 7i z 7 5i 3z 5i 7 (2i 3) Recuperatorio de Números Complejos 1. Determinar el valor de x, para que z 3 2 i 3 x i : a) sea un número real. b) sea un número imaginario puro. Tema A 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 5 3i b) 2 3i c) 2 e j 4 d) e j 3 4 3. Consideren los complejos: z1 2 3i ; z 2 4i ; z3 7 2i y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 Recuperatorio de Números Complejos 1. Determinar el valor de x, para que z 3 2 i 5 x i : a) sea un número real. b) sea un número imaginario puro. Tema B 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 2 7i b) 5 3i c) 3 e j 6 d) e j 2 3 3. Consideren los complejos: z1 2 5i ; z 2 2i ; z3 7 2i y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 Recuperatorio de Números Complejos 1. Determinar el valor de x, para que z 3 2 i 3 x i : a) sea un número real. b) sea un número imaginario puro. Tema A 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 5 3i b) 2 3i c) 2 e j 4 d) e j 3 4 3. Consideren los complejos: z1 2 3i ; z 2 4i ; z3 7 2i y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 Recuperatorio de Números Complejos 1. Determinar el valor de x, para que z 3 2 i 5 x i : a) sea un número real. b) sea un número imaginario puro. Tema B 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: a) 2 7i b) 5 3i c) 3 e j 6 d) e j 2 3 3. Consideren los complejos: z1 2 5i ; z 2 2i ; z3 7 2i y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 Evaluación de Números Complejos Tema A 1. Determinar el valor de x, para que 𝑧 = (−8 + 2𝑗17 ) ∙ (5 + 𝑥𝑗): a) sea un número real. b) sea un número imaginario puro. 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: 3𝜋 𝜋 a)−5 − 3𝑗 b) −2 + 3𝑗 c) 2⋅ ∠ (− 4 ) d) 1 ⋅ ∠ ( 4 ) 3. Consideren los complejos: 𝑧1 = −2 + 3𝑗; 𝑧2 = √−16; 𝑧3 = 7 + 2𝑗 y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 4. La suma de un n° complejos con su conjugado es 10 y la diferencia es 3j, ¿cuáles es el n° complejo? 5. Hallar un número complejo del 2do cuadrante que tiene por módulo 2 y tal que Re(z)=-1. Expresarlo en forma polar. Justificar gráficamente la solución. Evaluación de Números Complejos Tema B 1. Determinar el valor de x, para que 𝑧 = (3 − 5𝑗 23 ) ∙ (10 + 𝑥𝑗): a) sea un número real. b) sea un número imaginario puro. 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: 𝜋 2𝜋 a)2−7𝑗 b) 5 − 3𝑗 c) 3 ⋅ ∠ (− 6) d) 1 ⋅ ∠ ( 3 ) 3. Consideren los complejos: 𝑧1 = 2 − 5𝑗; 𝑧2 = √−25; 𝑧3 = −7 + 2𝑗 y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 4. La suma de un n° complejos con su conjugado es 6 y la diferencia es 7j, ¿cuáles es el n° complejo? 5. Hallar un número complejo del 4to cuadrante que tiene por módulo 4 y tal que Re(z)=3. Expresarlo en forma polar. Justificar gráficamente la solución. Evaluación de Números Complejos Tema A 1. Determinar el valor de x, para que 𝑧 = (−8 + 2𝑗17 ) ∙ (5 + 𝑥𝑗): a) sea un número real. b) sea un número imaginario puro. 2. Representar gráficamente los siguientes números complejos y también su conjugado de cada uno: 3𝜋 𝜋 a)−5 − 3𝑗 b) −2 + 3𝑗 c) 2⋅ ∠ (− 4 ) d) 1 ⋅ ∠ ( 4 ) 3. Consideren los complejos: 𝑧1 = −2 + 3𝑗; 𝑧2 = √−16; 𝑧3 = 7 + 2𝑗 y resuelvan las siguientes divisiones y multiplicaciones. Expresar el resultado en forma polar a) z1 z 2 b) z1 z3 c) z3 z2 e) 1 z1 f) z1 z 3 4. La suma de un n° complejos con su conjugado es 10 y la diferencia es 3j, ¿cuáles es el n° complejo? 5. Hallar un número complejo del 2do cuadrante que tiene por módulo 2 y tal que Re(z)=-1. Expresarlo en forma polar. Justificar gráficamente la solución.