Unidad 2 Teorema Fundamental del Cálculo Solución Hacemos x = t 1
Anuncio

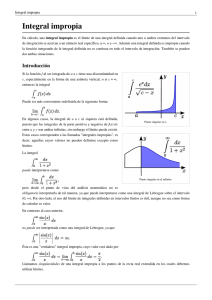
Unidad 2 Teorema Fundamental del Cálculo 2.2 Propiedades de la Integral Indenida Propiedades de la Integral Indenida (Método de Cambio de Variable) Proposición 1. Sea f una función denida en un intervalo I. Supongamos que ϕ es una función derivable con derivada continua. Si consideramos x = ϕ(t), donde t = ϕ−1 (x) de manera que Z Z f (ϕ(t))ϕ0 (t)dt f (x)dx = es decir si F es una primitiva de f y G es una primitiva de f (ϕ(t))ϕ0 (t) entonces F (x) = G(t) + c = G(ϕ−1 (x)) + c Demostración. Tenemos que G(ϕ−1 (x)) + c 0 = G0 ((ϕ−1 (x))(ϕ−1 )0 (x) = f (ϕ(ϕ−1 (x)))ϕ0 (ϕ−1 (x))(ϕ−1 )0 (x) Ahora bien 1 (ϕ−1 )0 (x) = ϕ0 (ϕ−1 (x)) por lo tanto −1 f (ϕ(ϕ 0 −1 (x)))ϕ (ϕ −1 0 (x))(ϕ por lo tanto ) (x) = f (ϕ(ϕ −1 0 −1 (x)))ϕ (ϕ (x)) 1 ϕ0 (ϕ−1 (x)) = f (x) G(ϕ−1 (x)) + c es una primitiva de f Ejemplo Usando el método de sustitución (Cambio de Variable) calcular Z √ dx √ x(1 + 3 x) Solución Hacemos x = t6 entonces 6t5 dt = dx y tenemos que Z √ dx √ = x(1 + 3 x) Z √ 6t5 √ 3 Z dt = 6t5 dt = 3 t (1 + t2 ) Z 6t2 dt = 6 1 + t2 Z t2 dt 1 + t2 t6 (1 + t6 ) Z 2 Z Z 2 Z t +1 1 1 t +1−1 dt = 6 − dt = 6 dt − dt =6 1 + t2 t2 + 1 t2 + 1 t2 + 1 √ √ = 6(t − arctan t + c) = 6( 6 x − arctan( 6 x) + c) Facultad de Ciencias UNAM Cálculo Diferencial e Integral II Prof. Esteban Rubén Hurtado Cruz 1 Unidad 2 Teorema Fundamental del Cálculo 2.2 Propiedades de la Integral Indenida Integrales Impropias Vamos a extender el concepto de integral a funciones no acotadas en un intervalo cerrado [a, b] y a funciones continuas en intervalos no acotados, a este tipo de integrales se les conoce como integrales impropias (Integral Impropia de 1er Clase) Denición 1. Si f (x) es continua en a < x < ∞ entonces ∞ Z b Z f (x)dx = lı́m f (x)dx b→∞ a a Denición 2. Si f (x) es continua en −∞ < x < b entonces Z a Z f (x)dx = lı́m a→−∞ −∞ b f (x)dx a Denición 3. Si f (x) es continua en −∞ < x < ∞ entonces Z ∞ Z a f (x)dx = −∞ Z f (x)dx + −∞ ∞ Z f (x)dx = lı́m a→−∞ a b Z f (x)dx + lı́m b→∞ a b f (x)dx a Si el limite existe, la integral impropia es convergente; si no, es divergente Ejemplo Vamos a comprobar la convergencia de las siguientes integrales Z ∞ 1 1 dx = lı́m b→∞ x2 b Z 1 1 1 b 1 1 dx = lı́m − 1 = lı́m − + =1 b→∞ b→∞ x2 x b 1 por lo tanto la integral impropia es convergente Ejemplo Calcular 0 Z −∞ Z ex dx tenemos que 0 ex dx = lı́m −∞ Z a→−∞ Z a 0 ex dx = lı́m ex |0a = lı́m e0 − ea = 1 − 0 = 1 a→−∞ a→−∞ ∞ 4 dx tenemos que (2|x| + 1)2 −∞ Z ∞ Z 0 Z ∞ 4 4 4 dx = dx + dx = 2 2 (2x + 1)2 −∞ (2|x| + 1) −∞ (−2x + 1) 0 Z 0 Z b 4 4 2 0 −2 b lı́m dx + lı́m dx = lı́m + lı́m a 0 a→−∞ a (−2x + 1)2 a→−∞ 1 − 2x b→∞ 0 (2x + 1)2 b→∞ 2x + 1 ! 2 2 −2 − −2 = lı́m − + lı́m =2+2=4 a→−∞ 1 − 2(0) b→∞ 1 − 2(a) 2(b) + 1 2(0) + 1 Ejemplo Calcular Facultad de Ciencias UNAM Cálculo Diferencial e Integral II Prof. Esteban Rubén Hurtado Cruz 2