Calcule la integral ∮ 3 + i + z dz donde C es el cırculo |z| = 10
Anuncio
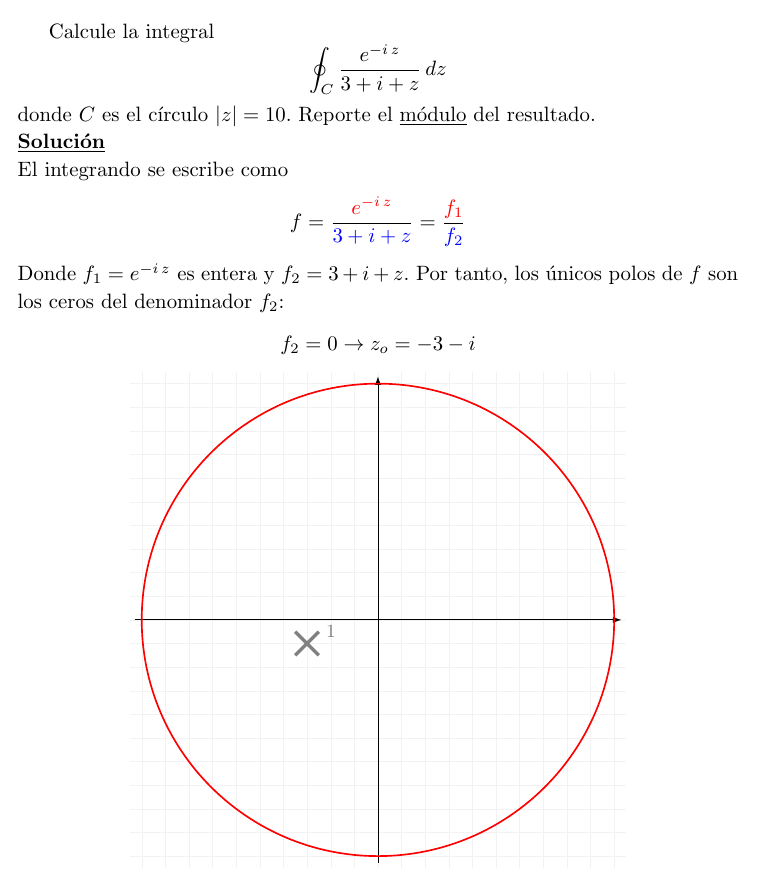
Calcule la integral I C e−i z dz 3+i+z donde C es el cı́rculo |z| = 10. Reporte el módulo del resultado. Solución El integrando se escribe como f= e−i z f1 = 3+i+z f2 Donde f1 = e−i z es entera y f2 = 3 + i + z. Por tanto, los únicos polos de f son los ceros del denominador f2 : f2 = 0 → zo = −3 − i 1 Como la curva de integración C es un cı́rculo con centro en z1 = 0 y radio r = 10 y la distancia de zo a z1 es √ d(zo , z1 ) = |z1 − zo | = | − 3 − i| = 4 ≈ 3.162 Entonces, el polo se encuentra dentro de C; por tanto, para calcular la integral debemos usar la fórmula de Cauchy: I e−i z dz = 2 π i [e−i,z ]z=−3−i C z − (−3 − i) Los cálculos se ilustran en la siguiente figura. Los cálculos se ilustran en la siguiente figura:











