Ecuaciones del mecanismo Cuadrilátero articulado

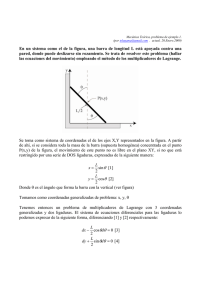
Ecuaciones del mecanismo
Cuadrilátero articulado
El eslabón 1 descansa sobre
la línea Y=0.
C
L3
3
4
B
L4
1
2
L2
D
A
L1
1
Parámetros e incógnitas
Como parámetros :
•Las longitudes de las barras L1,L2,L3,L4
•Las posiciones de los puntos fijos A y D
•valor de alpha
Como incógnitas :
•Las coordenadas del punto B
•Las coordenadas del punto C
Necesitamos 4 ecuaciones para darle solución al sistema
2
Ecuaciones del mecanismo
Cuadrilátero articulado
ì
ï
ü
xb - L2 cos w t
y b - L2 sen w t
(xc - xb )2 + ( y c - yb )2 ï
ï
Φ (q, t ) = í
ï
ï
ï ( x d - x c )2 + ( y d - y c
î
ï
ï
ï
ý =0
L ïï
) - L ïþ
2
2
3
2
4
Ya que :
Φ k (q, t ) = {q - w
0
t} = 0
3
Matriz Jacobiana
Compuesta por las derivadas parciales de las funciones respecto a
las incógnitas:
ê
é
1
0
0
0
ù
ú
0
1
0
0
ú
Φq = ê
ê - 2( xc - xb) - 2( yc - yb) 2( xc - xb)
2( yc - yb) ú
ê
ú
- 2( xd - xc) - 2( yd - yc)û
0
0
ë
4
Cálculo de velocidades
Para calcular la velocidad de los puntos, se plantea :
d Φ (q , t )
= 0 = Φ q q1 + Φ t
dt
Þ Φ q q1= - Φ t
é - 12 2 sin 3 ù
ê 12 cos q ú
2
ú
- Φt = ê
ê
ú
0
ú
ê
0
û
ë
Con la ventaja de que el Jacobiano ya está definido en el problema
de posición.
Además, este problema representa un sistema lineal, con lo que
se resuelve exactamente sin necesidad de utilizar Newton Raphson.
5
Cálculo de aceleraciones
Analogamente se plantea :
d 2 Φ (q , t )
=0Þ
2
dt
1 q q1 + Φ
1 t)
Φ qq
11= - (Φ
é - 1 2 L 2 cos 3 - a L 2 sin q ù
ê
- 1 2 L 2 sin q + a L 2 cos q
ê
- Φt =
ê
0
ê
0
êë
ú
ú
ú
ú
úû
Se debe definir una nueva matriz que es la derivada del jacobiano
respecto al tiempo (término a término) :
ê
.
Φq = ê
é
0
0
0
0
êë
ê
0
0
.
.
.
.
ê - 2( x c - x b ) - 2( y c - y b )
0
0
.
2( x c .
- 2( x d -
0
0
.
.
x b)
2( y c .
.
x c ) - 2( y d -
ù
ú
. ú
y b) ú
. ú
y c )úû
6