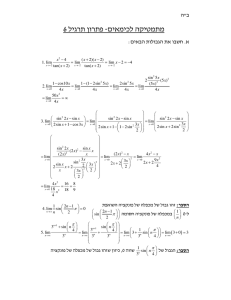
זהויות טריגונומטריות
Anuncio

זהויות טריגונומטריות
sin 2 α + cos 2 α = 1
tan 2 α
2
sin α =
1 + tan 2 α
1
cos 2 α =
1 + tan 2 α
(2k − 1)π
) = { ±} cos α , ∀ k ∈ Z
2
(2k − 1)π
cos(α +
) = { ±} sin α , ∀ k ∈ Z
2
(2k − 1)π
tan(α +
) = {±} cot α , ∀ k ∈ Z
2
(2k − 1)π
cot(α +
) = {±} tan α , ∀ k ∈ Z
2
sin(α + πk) = { ±} sin α ∀ k ∈ Z
sin(α +
cos(α + πk) = { ±} cos α ∀ k ∈ Z
:פונקציות טריגונומטריות של סכום והפרש ארגומנטים
sin( α + β ) = sin α cos β + sin β cos α
sin( α − β ) = sin α cos β − sin β cos α
cos(α + β ) = cos α cos β − sin α sin β
cos(α − β ) = cos α cos β + sin α sin β
tan α + tan β
tan(α + β ) =
1 − tan α tan β
tan α − tan β
tan(α − β ) =
1 + tan α tan β
:פונקציות טריגונומטריות של כפולה ארגומנטים
sin 2α = 2sin α cos α
cos 2α = cos 2 α − sin 2 α
2 tan α
tan 2α =
1 − tan 2 α
פונקציות טריגונומטריות של מחצית ארגומנטים
α 1 − cos α
=
2
2
α 1 + cos α
cos 2 =
2
2
sin 2
1
סכום והפרש של שתי פונקציות טריגונומטריות
α+β
α−β
cos
2
2
α−β
α+β
sin α − sin β = 2sin
cos
2
2
α+β
α−β
cos α + cos β = 2cos
cos
2
2
α+β
α−β
cos α − cos β = −2sin
sin
2
2
sin α + sin β = 2sin
המעבר מכפל לסכום או הפרש פונקציות
1
sin α sin β = − (cos(α + β ) − cos(α − β ))
2
1
cos α cos β = (cos(α + β ) + cos(α − β ))
2
1
sin α cos β = (sin(α + β ) + sin(α − β ))
2
הצבה אוניברסאלית
α
2
sin α =
2 α
1 + tan
2
α
1 − tan 2
2
cos α =
2 α
1 + tan
2
2 tan
זווית נוספת
a +b
2
2
a
⎛
⎞
a
b
a cos α + b sin α = a 2 + b 2 ⎜
cos α +
sin α ⎟ =
2
2
a2 + b2
⎝ a +b
⎠
= a 2 + b 2 ( sin β cos α + cos β sin α ) = a 2 + b 2 ⋅ sin(α + β )
β
b
2