6 תרגיל פתרון - מתמטיקה לכימאים
Anuncio
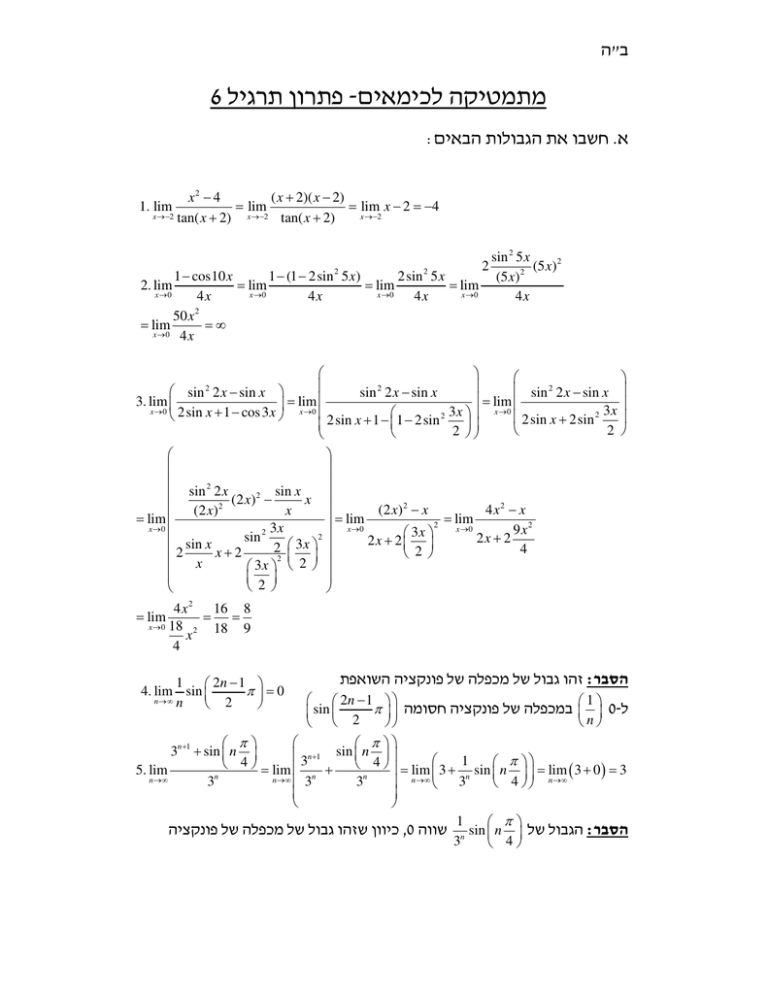
ב"ה 6 מתמטיקה לכימאי פתרו תרגיל : חשבו את הגבולות הבאי.א x2 − 4 ( x + 2)( x − 2) = lim = lim x − 2 = −4 x →−2 tan( x + 2) x →−2 x →−2 tan( x + 2) 1. lim sin 2 5 x (5 x)2 2 1 − cos10 x 1 − (1 − 2sin 2 5 x) 2sin 2 5 x (5 x) 2. lim = lim = lim = lim x→0 x →0 x →0 x→0 4x 4x 4x 4x 2 50 x = lim =∞ x→0 4 x 2 2 sin 2 2 x − sin x sin 2 x − sin x sin 2 x − sin x = lim 3. lim = lim x → 0 2sin x + 1 − cos 3 x x →0 2sin x + 1 − 1 − 2sin 2 3 x x →0 2sin x + 2sin 2 3 x 2 2 2 2 sin 2 x (2 x)2 − sin x x (2 x)2 (2 x) 2 − x 4 x2 − x x = = = lim lim lim x →0 2 x→0 x →0 3x 9 x2 3x 2 sin 2 x + 2 2 x + 2 2 2 3x 4 2 sin x x + 2 2 2 x 3x 2 2 2 4x 16 8 = lim = = x → 0 18 2 18 9 x 4 1 2n − 1 4. lim sin π=0 n →∞ n 2 זהו גבול של מכפלה של פונקציה השואפת:הסבר 2n − 1 1 π במכפלה של פונקציה חסומה 0ל sin n 2 π π 3n +1 + sin n sin n n +1 4 = lim 3 + 4 = lim 3 + 1 sin n π = lim 3 + 0 = 3 5. lim ( ) n n n →∞ n →∞ 3 3n 3n 3 n →∞ 4 n →∞ 1 π כיוו שזהו גבול של מכפלה של פונקציה,0 שווהn sin n הגבול של:הסבר 3 4 ב"ה π sin n במכפלה של פונקציה חסומה 4 1 n 0השואפת ל 3 : חשבו את הנגזרות של הפונקציות הבאות.ב 1 1 1. y ' = 3sin 2 cot x ⋅ cos cot x ⋅ − 2 ⋅ sin x 2 x ( = ) ( ( ) ) ( −3sin 2 cot x ⋅ cos cot x 2 x ⋅ sin 2 ) x −2 x 1 ⋅ − sin ⋅ = 2 x 2 2 cos 2 1 1 x 3. y ' = 3 x 2 arcsin + x 3 ⋅ ⋅ 2 2 x 2 1− 2 1 1 4 x 3 arctan x − x 4 ⋅ ⋅ 1 + x2 2 x 4. y ' = 2. y ' = 2 x cos 2 1 ln 2 ⋅ ( arctan x ) cos x 2 ln 2 ⋅ sin 4 cos x 2 x 2 2 ( ) 1 x − cos x (1 + sin x ) − cos x (1 − sin x ) 5. y ' = 4 cos3 ( sin ( ln x ) ) ⋅ − sin ( sin ( ln x ) ) ⋅ cos ( ln x ) ⋅ 1 1 ⋅ ⋅ 2 1 − sin x 1 − sin x 1 + sin x ) ( 2 1 + sin x 1 + sin x 1 + sin x −2 cos x cos x cos x 1 = ⋅ = = = 2 2 2 2 (1 − sin x ) (1 + sin x ) 1 − sin x cos x cos x 6. y ' = 1 ′ 2 1 cot x − 1 7. y ' = ( ln sin x ) 3 = ( ln sin x ) 3 ⋅ ⋅ cos x = 2 sin x 3 3 3 ( ln sin x ) 8. y ' = 1 1+ x 1+ 1− x 2 ⋅ 1(1 − x ) + (1 + x ) (1 − x ) (1 − x ) 2 ⋅ 2 2 2 (1 − x ) + (1 + x ) (1 − x ) 2 2 = = 1 = 1+ (1 − x ) 2 (1 + x 2 2 ⋅ ⋅ 2 2 2 = 1 1 + x2 (1 + x ) (1 − x ) 2 (1 − x ) 2 ) (1 − x ) 2 = 1 ⋅ 2 (1 − x ) + (1 + x ) (1 − x ) 2 (1 − x ) 2 2 2 ב"ה 9. y′ = 10 ln 9 2x − 1 x + 34 − x x + 34 + x 2 x 2 + 34 ⋅ ⋅ x 2 + 34 + x x 2 + 34 − x 2 2 ( ) ( x 2 + 34 + x − ( ) 2x x 2 + 34 − x + 1 2 2 x + 34 x 2 + 34 + x ) 2 : כלומר, x 2 + 34 = t לצור נוחות כתיבת פתרו התר' נסמ 2x 2x − 1 ( t + x ) − ( t − x ) + 1 t − x t + x 2t 2t y′ = 10 ln 9 ⋅ ⋅ 2 t+x t−x t + x ( ) t−x t+x = 10 ln 9 ⋅ ⋅ t+ x t−x x+ x2 x2 x2 −t − x − x −t + + x 2 − 2t t−x t+x t t = 10 ln 9 ⋅ t 2 ⋅ 2 t + x t − x (t + x ) (t + x ) x2 2 x 2 2t 2 − 2t − t−x 1 9t−x t t t = 10 ln 9 ⋅ ⋅ = ⋅ 10 ln 2 2 t+ x t−x t+x t+ x t −x 2 2 ( x2 − t 2 ) t−x t = 10 ln 9 ⋅ 2 2 t+ x t −x t − x −2 = 10 ln 9 ⋅ t+x t : ונקבל, x 2 + 34 = t כעת נציב חזרה x 2 + 34 − x −2 y′ = 10 ln 9 ⋅ x 2 + 34 + x x 2 + 34








