Espacio vectorial de..
Anuncio

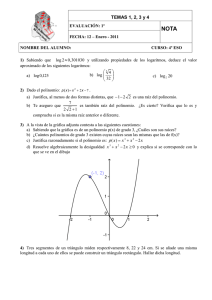
En el espacio R e vectorial real C (1; e), se de…ne el producto escalar (f; g) = 1 (log x) f (x) g (x) dx p (a) Calcula la norma de la función x: (b) Encuentra un polinomio lineal g (x) = a + bx que sea ortogonal a la función f (x) = 1: Solución: (a) La p de la función se de…ne como p norma j xj = (x; x) así Re p que 2 j xj = (x; x) = 1 (log x) xdx = 41 e2 + 14 por p tantop j xj = 12 e2 + 1 = 1: 45 (b) El producto escalar de 1 con el polinomio g (x) = a + bx está dado por Re (1; a + bx) = 1 (log x) (a + bx) dx = a + 41 b + 14 be2 Si queremos que sean ortogonales, debemos tener (1; a + bx) = 0 o sea a + 14 b + 41 be2 = 0 que tiene como solución a = 14 1 + e2 b El polinomio requerido es entonces p (x) = 14 1 + e2 b + bx con b arbitrario 1