La geometría del triángulo, el software de Geometría Dinámica e

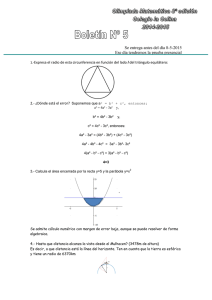
La Gaceta de la RSME, Vol. 13 (2010), Núm. 3, Págs. 557–569
557
Educación
Sección a cargo de
María José González
¿Sabían que en un triángulo rectángulo la diferencia entre los dos ángulos agudos es igual al ángulo comprendido entre la altura y la mediana
relativas a la hipotenusa? Se trata de una propiedad enunciada por Severi en 1952 y forma parte de la impresionante colección de propiedades y
pruebas sobre la geometría del triángulo que Ricardo Barroso ha recopilado en la web http: // personal. us. es/ rbarroso/ trianguloscabri/ .
La labor constante que este profesor viene desarrollando desde hace 10
años ha agrupado más de 560 enunciados con sus correspondientes pruebas, varias para cada enunciado, todo ello aportado por colaboradores y
lectores de su web. Así, ha contribuido a consolidar una comunidad virtual de usuarios que comparten ideas para que se siga incrementando el
conocimiento sobre esta sencilla y sorprendente figura.
La geometría del triángulo, el software de Geometría
Dinámica e Internet: Una integración posible
por
Ricardo Barroso Campos
1.
El laboratorio virtual de triángulos con Cabri
El Año Mundial de las Matemáticas, año 2000, se fundó en Internet el Laboratorio virtual de triángulos con Cabri, al que nos referiremos en lo que sigue como
el Laboratorio. Se trata de una revista digital de acceso libre que se publica en
la web http://personal.us.es/rbarroso/trianguloscabri/ y que nació con la
pretensión de realizar una labor de recopilación e investigación sobre la geometría
del triángulo aprovechando el apoyo de la geometría dinámica.
Así pues, hace ya 10 años que se viene publicando esta revista de periodicidad
quincenal en la que participan especialistas, tanto enviando problemas para publicar,
como solucionando los enunciados propuestos. Si bien inicialmente se intentó que las
soluciones aportadas estuviesen basadas en construcciones realizadas con el software
558
Educación
Cabri-Géomètre, con el paso del tiempo se han ido incorporando otros tipos de
software y también se han incluido las variadas soluciones, de todo tipo, que han
aportado lectores y colaboradores de la revista. Así, lo más frecuente es que cada
problema tenga varias soluciones. En la Figura 1 se puede ver el enunciado de uno
de los problemas de la segunda quincena de junio de 2010.
Figura 1: Enunciado de uno de los problemas del Laboratorio.
Esta idea ha prosperado gracias a dos herramientas tecnológicas. Por un lado,
el software de Geometría Dinámica, que ha propiciado la búsqueda de propiedades
La Gaceta ? Secciones
559
geométricas nuevas y ha dado ideas para su posterior demostración formal. Por otro
lado, Internet se ha constituido en el medio que nos permite la disponibilidad inmediata de las ediciones de la revista, la libre distribución a los interesados, el feedback
necesario con los lectores, el intercambio de pareceres y opiniones con los colaboradores, la recepción de soluciones a los problemas planteados, y las aportaciones de
nuevas propuestas.
1.1.
Comunidad Virtual de Matemáticas sobre la Geometría del triángulo
La comunicación a través de Internet ha permitido la creación y consolidación de
una comunidad de carácter internacional con intereses en la geometría del triángulo.
Los miembros de esta comunidad se agrupan en dos grandes bloques:
1. Un primer bloque lo integran los investigadores matemáticos de los niveles
educativos medio, superior y de posgrado, sea cual sea el área disciplinaria en
la que laboran; este bloque lo conforman docentes y no docentes cuya formación
académica inicial no es necesariamente de matemáticas.
2. El otro bloque está integrado por profesores que se dedican exclusivamente a
la docencia y les interesa conocer los resultados y soluciones que aparecen en
Internet, así como por los estudiantes que aprenden matemáticas a través de
los mismos cauces.
En estos diez años la Comunidad Virtual que se ha constituido en torno a esta idea
se puede considerar polifacética, puesto que incorpora variadas y amplias maneras
de intervención:
Internautas que visitan la página web simplemente para informarse, aunque
no envían propuestas ni soluciones.
Colaboradores ocasionales, que han enviado alguna propuesta de un problema
o de solución.
Colaboradores que envían soluciones con asiduidad.
Colaboradores que envían propuestas de problemas, tanto comunicaciones personales como vinculadas a determinada bibliografía.
Por último, también participan colaboradores que no desean que se publique
su nombre y, desde el anonimato, hacen aportaciones y sugerencias.
En este periodo ha habido más de 113 colaboradores españoles, franceses, italianos, peruanos, colombianos, mejicanos, venezolanos y argentinos. Se han producido
cerca de 200 000 visitas de más de 30 países.
2.
La esencia del Laboratorio: los problemas y sus variadas soluciones
El Laboratorio se ha ido alimentando de las aportaciones de colaboradores hasta
publicar, durante este tiempo, más de 560 problemas, con una gran diversificación de
560
Educación
fuentes bibliográficas que incluye más de 300 referencias, entre las que destacamos
las que se describen en la sección siguiente. Las diversas soluciones que se han ido
obteniendo para cada problema se encuentran clasificadas por años académicos en
el enlace Cursos de la página web.
2.1.
Las fuentes de los problemas sobre el triángulo
La bibliografía específica de la geometría del triángulo, dentro de la matemática,
no parecía amplia, pero a medida que fuimos buscando aparecieron autores consagrados que habían tratado el tema y, a su vez, citaban en sus referencias a otros.
De esta forma, poco a poco, fueron surgiendo libros dedicados exclusivamente a este ámbito, algunos antiguos, como el caso de La recente geometria del triangolo de
Cristoforo Alasia (1900) [1], y otros más recientes, como La géométrie du triangle de
Yvonne Sortais y René Sortais (1997) [16]. También fueron apareciendo foros en Internet que planteaban discusiones específicas, como Hyacinthos1 (1999–2010), creado
por Antreas P. Hatzipolakis en honor al geómetra francés Emile Michel Hyacinthe
Lemoine.
También se han utilizado trabajos de reconocidos matemáticos que han dedicado
atención a la geometría del triángulo, entre los que cabe mencionar a Rey Pastor
[14], Puig Adam [13], De Guzmán [9], Ramanujan [4], Pólya [12] o Lewis Carroll [5].
Otra de las principales fuentes para obtener problemas ha sido la tesis de maestría
de Martha Iglesias [10], Curso de Resolución de Problemas Geométricos Asistido por
Computadora, que fue realizada bajo la tutoría de la profesora Mireles en la Universidad Pedagógica Experimental Libertador de Maracay (Venezuela). Las propuestas
de este trabajo se ajustaban de manera total al propósito del Laboratorio.
Revistas de prestigio internacional como The American Mathematical Monthly
(MAA) o Crux Mathematicorum with Mathematical Mayhem (CMS) también han
tratado este tema.
Páginas web cuyo foco de interés es la geometría del triángulo, como la Enciclopedia de los centros del triángulo2 (ETC) de Clark Kimberling, que cuenta con un
catálogo de 3587 puntos que son centros relacionados con el triángulo, o dedicadas a
problemas matemáticos como las revistas digitales Kömal3 o Mathematical Reflections4 , han sido referentes para el trabajo realizado y, en alguna ocasión, han dado
cuenta de los resultados obtenidos. Por ejemplo, para la ETC, el centro X(155) está
dedicado al español Jordi Dou, cuya circunferencia se trató en el Problema 55 del
Laboratorio en 2002:
Dado el triángulo ABC, construir un círculo que corte a las rectas BC, CA
y AB en pares de puntos A0 y A00 , B 0 y B 00 , y C 0 y C 00 , respectivamente, tal
0 AA00 , B\
0 BB 00 y C\
0 CC 00 sean rectos.
que los tres ángulos A\
La solución que aportó el profesor Dou en 1986 se publicó en el Laboratorio5 .
1 http://tech.groups.yahoo.com/group/Hyacinthos/
2 http://faculty.evansville.edu/ck6/encyclopedia/ETC.html
3 http://www.komal.hu/info/bemutatkozas.e.shtml
4 http://reflections.awesomemath.org
5 http://www.aloj.us.es/rbarroso/trianguloscabri/sol/soldoufinal.htm
561
La Gaceta ? Secciones
En la Figura 2 podemos ver la imagen que acompaña a la traducción al inglés de
esta solución que apareció en la revista Crux Mathematicorum [7] en noviembre de
20026 . La circunferencia Ω es la solución buscada.
Figura 2: Circunferencia de Dou.
Otra fuente de información proviene de las Olimpiadas Internacionales de Matemáticas7 (IMO), que se vienen celebrando desde 1959, año en que las organizó
Rumanía. Los equipos que preparan los problemas que se proponen suelen incorporar problemas de la geometría del triángulo. Así, por ejemplo, el siguiente enunciado
corresponde al Problema 60 del Laboratorio, y fue propuesto en la Primera IMO:
Construya un triángulo rectángulo con hipotenusa dada tal que la mitad de
la longitud de la misma sea la media geométrica de sus catetos.
2.2.
Tipos de problemas
La secuenciación seguida en el Laboratorio ha variado a lo largo de estos diez
años. La primera opción fue aportar un problema quincenal que, más tarde, se amplió
a dos, con la idea de distinguir entre problemas para el aula y problemas para la
investigación. Un problema para el aula sería aquel problema que claramente puede
enunciarse y resolverse en un tiempo adecuado al horario escolar, aproximadamente
una hora. Por ejemplo, el texto siguiente es el Problema 197 del Laboratorio, y lo
enunció Severi en 1952 [15]:
6 http://www.aloj.us.es/rbarroso/trianguloscabri/sol/dou1140.pdf
7 http://www.artofproblemsolving.com/Wiki/index.php/1959_IMO_Problems
562
Educación
En un triángulo rectángulo la diferencia de dos ángulos agudos es igual al
ángulo comprendido entre la altura y la mediana relativa a la hipotenusa.
La prueba de esta propiedad8 usa resultados de geometría básica: basta inscribir
el triángulo en una circunferencia y trabajar con las propiedades de ángulos centrales
e inscritos (véase la Figura 3).
Figura 3: Prueba al problema de Severi, aportada al Laboratorio por Francisco
Javier García Capitán.
Un problema para la investigación sería un problema abierto, donde hubiese preguntas de tipo alternativo para que el investigador las resolviese, y pudiese plantear
cuestiones e ir desgranando respuestas a las mismas. Por ejemplo, el enunciado siguiente se publicó como Problema 514 en junio de 2009 en el Laboratorio y aparece
en [8]:
Se sabe que la circunferencia circunscrita al triángulo formado por las tres
tangentes a la parábola pasa por un punto fijo. ¿Caracteriza esta propiedad
a la parábola?
La solución aportada para este problema por Vicente Vicario García9 es de tipo analítico y va enlazando distintas propiedades que, a su vez, tienen su propia
demostración.
En los ejemplos que hemos mostrado hasta el momento, vemos que algunos enunciados buscan un cálculo concreto (por ejemplo, el Problema 569 que mostramos
antes (Figura 1)), otros solicitan una construcción (Problemas 55 y 60), otros demandan la demostración de una propiedad dada como cierta (Problema 197), otros
establecen una conjetura que invita a la investigación (Problema 514). No obstante,
la distinción entre estos tipos de problemas era difícil de delimitar en muchos casos,
por lo que esta clasificación se terminó abandonando.
8 http://www.aloj.us.es/rbarroso/trianguloscabri/sol/sol197garcap.htm
9 http://personal.us.es/rbarroso/trianguloscabri/sol/sol514vic.htm
563
La Gaceta ? Secciones
Más adelante, a medida que se iban recibiendo más colaboraciones, se fue aumentado el número de problemas que se proponía, llegando en la actualidad a publicar
unos cuatro problemas por quincena.
2.3.
La variedad de soluciones
Casi todos los problemas propuestos han sido solucionados por lectores y colaboradores. En estos momentos, sólo quedan tres problemas pendientes de resolver, que
pueden encontrarse en el enlace Por resolver 10 de la web del Laboratorio. Consideramos que el compendio de resultados obtenido es el fruto de una labor investigadora
colectiva de alto nivel, ya que se han recibido más de 1500 soluciones para los más de
560 problemas propuestos. Es de señalar que 7 de los 113 colaboradores han mantenido una participación constante y enriquecedora, enviando más de cien propuestas,
entre soluciones y enunciados. Otro grupo de 47 colaboradores, por el contrario,
sólo han enviado una propuesta (enunciado o solución) y constituyen un grupo de
internautas que han visitado ocasionalmente la página web del Laboratorio.
Algunos problemas han dado lugar a muy variadas estrategias de solución. Así,
por ejemplo, el Problema 105 siguiente se publicó el 1 de julio de 2003 y tuvo siete
soluciones11 :
En el desierto del Sahara y en tres puntos A, B, C, que forman los vértices
de un triángulo equilátero de 700 km de lado, se encuentran tres vehículos
cuyas velocidades respectivas son de 20 km/h, 40 km/h y 60 km/h. Comunicados por radio con el centro de operaciones, reciben la orden de partir
para reunirse lo antes posible. ¿Dónde está situado el punto de la reunión?
Este problema, de enunciado sencillo, ejemplifica de manera concreta las enormes
posibilidades y amplia versatilidad de la geometría para utilizar diferentes estrategias
de resolución de un problema. La variedad de métodos de resolución fue la siguiente:
1. Usando que la suma de las distancias desde un punto cualquiera de una circunferencia hasta los dos vértices más próximos de un triángulo equilátero inscrito
en esta circunferencia, es igual a la distancia hasta el vértice más lejano.
2. Realizando el problema de forma experimental con Cabri.
3. Haciendo un planteamiento proporcional.
4. Aplicando el teorema de los senos.
5. Usando Derive.
6. Usando la circunferencia de Apolonio.
7. Utilizando una bisectriz y una mediatriz: en la Figura 4 se puede ver la construcción en Cabri-Géomètre del punto P buscado. Por el teorema de la bisectriz
\
interior, se sabe que la bisectriz de AP
B dividirá al segmento AB en dos partes
10 http://personal.us.es/rbarroso/trianguloscabri/prosinres.htm
11 Puede consultarse el detalle
trianguloscabri/curso0203.htm
de
las
mismas
en
http://personal.us.es/rbarroso/
564
Educación
proporcionales BT = 2 T A, con T en el segmento AB. Por otra parte, sabemos
que la bisectriz de un ángulo se corta con la mediatriz del lado opuesto en un
punto de la circunferencia circunscrita; en este caso, dicha mediatriz es la de
AB, que corta a la circunferencia en C. Por tanto, la bisectriz que buscamos es
la recta CT , que cortará de nuevo a la circunferencia en el punto P buscado.
Figura 4: Problema del desierto, argumentando con la mediatriz y la bisectriz.
3.
3.1.
La utilidad de la tecnología
El software de Geometría Dinámica y los descubrimientos en
Geometría
La utilización de Software de Geometría Dinámica ha servido para ampliar notablemente las relaciones y propiedades que se conocían sobre la geometría del triángulo. Basten dos ejemplos, que han sido tratados en el Laboratorio, para mostrar
esta afirmación. La cubierta de febrero de 1992 de Mathematics Teacher mostraba que si las terceras partes de los lados de un triángulo equilátero se unen a los
vértices opuestos, el área del triángulo central es la séptima parte del área del triángulo original. En una carta a la revista en marzo de 1993, Joe Kennedy señalaba
que tal restricción a un triángulo equilátero no era necesaria. Hace alrededor de un
año, Marion Walter12 , utilizando el programa Geometer’s Sketchpad, descubrió el
siguiente resultado, llamado Teorema de Marion Walter en su honor, que tratamos
en el Problema 485 del Laboratorio:
12 http://www2.edc.org/makingmath/mathprojects/marionwalter/links/marionwalter_lnk_1.
asp
La Gaceta ? Secciones
565
Si los puntos que dividen cada lado de un triángulo en tres partes iguales
se unen al correspondiente vértice opuesto, se forma un hexágono cuya área
es la décima parte del área del triángulo. [6]
La construcción de la circunferencia de Lester, tratada en el Problema 15 del
Laboratorio, constituye un excelente enriquecimiento de la geometría en secundaria,
especialmente cuando se aborda con un programa de Geometría Dinámica. Se considera un triángulo escaleno y se construyen los cuatro puntos especiales siguientes:
su circuncentro, el centro de la circunferencia de los nueve puntos, el primer punto
de Fermat y el segundo punto de Fermat. El Teorema de Lester afirma que hay
una circunferencia que pasa por estos cuatro puntos. Los estudiantes saben que tres
puntos no colineales determinan una circunferencia, así que cuando cuatro puntos
especiales están sobre una circunferencia, ¡entonces tenemos un teorema!
Estas muestras señalan el proceso de descubrimiento que debe ir seguido, según
Piaget y García [11], del proceso de justificación. Este aspecto se ha tratado con
detalle en [3].
3.2.
Los Applets
Dado que Internet es un medio activo, en la revista se incorporaron los applets
de Cabri-Géomètre que permiten al usuario una acción directa y una manipulación
de las figuras manteniendo el principio de la geometría dinámica, es decir, al actuar
sobre los elementos libres de la figura se mantienen las relaciones establecidas y
se observan las propiedades geométricas que permanecen. Así, en julio de 2002,
se informaba a los visitantes de que se iban a usar los applets de CabriJava, que
permiten, sin necesidad de tener Cabri en el ordenador, manipular y visualizar la
figura.
Clicando dos veces sobre la ventana de uno de dichos applets aparece una barra
de menú en la parte inferior que permite (ver Figura 5):
1. Situar la construcción en el momento del proceso de construcción que deseemos
y reconstruirla.
2. Retroceder o avanzar paso a paso en la construcción.
3. Desplazar la zona de trabajo en la que está realizada la figura.
4. Dibujar las trazas de una figura.
5. Realizar animación automática.
6. Bajar la figura al ordenador local.
Si volvemos a clicar, desaparece el menú y podemos arrastrar algunos objetos de
la figura.
566
Educación
Figura 5: Un applet de CabriJava.
4.
Usos del Laboratorio
El Laboratorio ha catalogado más de 315 propiedades, relaciones y tipos de
triángulos, y ha clasificado los problemas en un catálogo13 . Consideramos que esa
clasificación puede ser útil en el proceso de enseñanza/aprendizaje de la geometría.
Así, si un profesor desea, por ejemplo, explicar la perpendicularidad en el plano,
podría buscar entre los diecisiete problemas en los que aparece esta idea. Por ejemplo, el Problema 276, tomado de Aref y Wernick [2], hace intervenir numerosas
propiedades relacionadas con la idea de perpendicularidad:
O es un punto sobre la circunferencia circunscrita al triángulo ABC. Demostrar que si las perpendiculares desde O a los lados AB, AC y BC cortan
a la circunferencia en los puntos c, b y a, el triángulo abc es igual al ABC.
También, con el propósito de que los estudiantes desarrollen su capacidad investigadora, se pueden proponer problemas motivadores, como el Problema 77, que
da lugar a una caracterización peculiar de la noción de triángulo equilátero:
Un triángulo ABC es equilátero si tomado un punto interior P cualquiera,
se puede construir un triángulo con las longitudes P A, P B y P C.
13 http://personal.us.es/rbarroso/trianguloscabri/propiedades1al.htm
La Gaceta ? Secciones
5.
567
Algunos datos más sobre el Laboratorio
Los problemas y las soluciones remitidos al Laboratorio son evaluados por un
Comité Editorial que se renueva cada dos años y analiza todas las propuestas, valorando especialmente la corrección de las soluciones y dando indicaciones sobre
posibles errores.
La página web del Laboratorio tiene una estructura que permite navegar de
manera fácil a colaboradores, investigadores, profesores y estudiantes. En la página
de inicio aparecen los problemas de la quincena y sus soluciones, la composición del
Comité Editorial, las normas de participación y el registro ISSN. Además hay un
menú con distintos ítems:
Editoriales: El Comité Editorial especifica los móviles e intereses que orientan
esta labor.
Cursos: Los problemas y las soluciones recibidas se reúnen en cursos académicos, comenzando en septiembre y terminando en agosto del año siguiente. A
cada problema se le identifica con tres o cuatro palabras clave que permitan
captar la esencia del mismo.
Por resolver: Aparecen los problemas que aún no se han resuelto. Su número
ha ido variando y, a veces, se ha tardado hasta cinco años en resolver alguno
de ellos.
Referencias en Internet: En Internet hay 32 referencias españolas y 22 internacionales que citan el Laboratorio y que se van actualizando con el tiempo.
Resumen. Este apartado está subdividido en varios ítems:
• Enunciados: Aparecen solo los enunciados de los problemas.
• Colaboradores: Se han colocado los colaboradores por orden alfabético y
se precisa cuáles han sido sus aportaciones.
• Bibliografía: Aparecen los problemas vinculados a las fuentes bibliográficas utilizadas (libros, revistas, internet, comunicaciones personales, etc).
• Propiedades: Se enuncian las propiedades, relaciones geométricas y tipos de triángulos tratados, con la correspondiente catalogación de los
problemas en los que aparecen. Alineaciones de tres puntos, alturas, ángulos, área, bisectriz interna, circunferencia, construcción de triángulos
que cumplen determinadas propiedades, medianas, triángulo equilátero y
triángulo rectángulo, son las más utilizadas.
Con motivo de la publicación de los problemas centenarios, se ha dado la posibilidad a los investigadores de publicar artículos para profundizar en relaciones y
propiedades del triángulo. De esta manera, han visto la luz 24 artículos con muy
variada información, que han sido escritos por diez autores.
6.
Comentarios finales
La presencia cada vez mayor de Internet en el panorama investigador, con la
facilidad para la comunicación que conlleva, junto con el uso en la enseñanza y
568
Educación
en la investigación del software de geometría dinámica, han propiciado que se haya
ampliado considerablemente el conjunto de propiedades y relaciones geométricas que
involucran a una figura tan elemental como es el triángulo.
Desde la consideración de que este trabajo debe ser conocido entre los investigadores y el público que se interese por la Ciencia, se han realizado distintas presentaciones para difundirlo. Así, el Laboratorio se ha presentado en el V Congreso
de la Sociedad Española de Investigación en Educación Matemática celebrado en
Almería en 2001, en la Semana de la Ciencia y la Tecnología de 2003 y 2009, evento patrocinado entre otras entidades por la Fundación Española para la Ciencia
y la Tecnología, o en la VIII Feria Madrid es Ciencia de 2007, organizado por la
Comunidad de Madrid, con el apoyo de la Universidad de Sevilla.
La modesta contribución que se pretendía, hace 10 años, con el nacimiento del
Laboratorio, ha desbordado las expectativas iniciales. El amplio registro de problemas de que se dispone y la variedad de soluciones que se aportan hace pensar que el
trabajo emprendido el año 2000 pueda tener continuidad en el tiempo. Animamos a
todos los lectores a contribuir a que esto sea posible.
Referencias
[1] C. Alasia, La recente geometria del triangolo. San Lapi, Cittá di Castello,
1900.
[2] M. N. Aref y W. Wernick, Problems & Solutions in Euclidean Geometry.
New York: Dover Publications, 1968.
[3] R. Barroso, Cabri II come rivelatore di scoperte in geometria: discussione di
un caso. La Matematica e la sua Didattica 1 (2008), 123–134.
[4] B.C. Bernd, Ramanujan’s Noteboooks, Part IV. New York: Springer Verlag,
1994.
[5] L. Carroll, Problemas de almohada. Madrid: Nivola, 2005.
[6] A. Cuoco, P. Goldenberg y J. Mark, Reader Reflections. Marion’s Theorem. The Mathematics Teacher 86 (8) (1993), 619.
[7] J. Dou, Problem 1140. Crux Mathematicorum 28 (2002), 461–462.
[8] J. Gallego-Díaz, Nuevos problemas de matemáticas. Madrid: Editorial Norte
y Sur, 1965.
[9] M. de Guzmán, Mirar y ver. Madrid: Alhambra, 1977.
[10] M. Iglesias, Curso de Resolución de Problemas Geométricos Asistido por
Computadora. Tesis de maestría. Universidad Pedagógica Experimental Libertador, Instituto Pedagógico de Maracay, Venezuela, 2000.
[11] J. Piaget y R. García, Psicogénesis e historia de la ciencia. México: Siglo
XXI, 1982.
[12] G. Pólya, Cómo plantear y resolver problemas. México: Editorial Trillas, 1965.
[13] P. Puig Adam, Curso de Geometría Métrica I, Fundamentos. Madrid: Euler,
1986, 16 ed.
La Gaceta ? Secciones
569
[14] J. Rey Pastor, Curso Cíclico de Matemáticas. Madrid-Buenos Aires, 1930,
2 ed.
[15] F. Severi, Elementos de geometría. Barcelona: Editorial Labor, 1952.
[16] Y. Sortais y R. Sortais, La géométrie du triangle. Paris: Hermann, 1997.
Ricardo Barroso Campos, Dpto. de Didáctica de las Matemáticas, Universidad de Sevilla
Correo electrónico: rbarroso@us.es
Página web: http://personal.us.es/rbarroso/